已知圆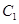 的方程为
的方程为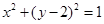 ,定直线
,定直线 的方程为
的方程为 .动圆
.动圆 与圆
与圆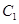 外切,且与直线
外切,且与直线 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹 的方程;
的方程;
(2)直线 与轨迹
与轨迹 相切于第一象限的点
相切于第一象限的点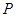 , 过点
, 过点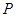 作直线
作直线 的垂线恰好经过点
的垂线恰好经过点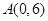 ,并交轨迹
,并交轨迹 于异于点
于异于点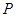 的点
的点 ,求直线
,求直线 的方程及
的方程及 的长.
的长.
已知函数 (
( ).
).
(1)当 时,求函数
时,求函数 在
在 上的最大值和最小值;
上的最大值和最小值;
(2)当函数 在
在 单调时,求
单调时,求 的取值范围;
的取值范围;
(3)求函数 既有极大值又有极小值的充要条件。
既有极大值又有极小值的充要条件。
等差数列 的各项均为正数,
的各项均为正数, ,前
,前 项和为
项和为 ,
, 为等比数列,
为等比数列, 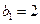 ,且
,且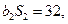
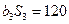 .
.
(1)求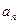 与
与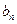 ;
;
(2)求数列 的前
的前 项和
项和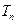 。
。
(3)若 对任意正整数
对任意正整数 和任意
和任意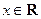 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
如图,在长方体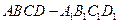 中,
中,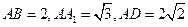 ,
, 为
为 的中点,
的中点, 为
为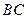 的中点。
的中点。
(1)证明: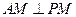 ;
;
(2)求 与平面
与平面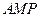 所成角的正弦值。
所成角的正弦值。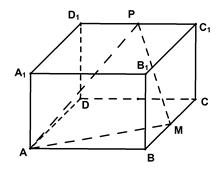
(本小题满分12分)
设进入某商场的每一位顾客购买甲种商品的概率为 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望。
的分布列及期望。
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,且满足
,且满足 ,
, 。
。
(1) 时,若
时,若 ,求
,求 的面积.
的面积.
(2)求 的面积等于
的面积等于 的一个充要条件。
的一个充要条件。