(本小题满分12分)
设进入某商场的每一位顾客购买甲种商品的概率为 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望。
的分布列及期望。
(本小题满分12分)
已知圆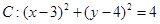 和直线
和直线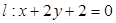 ,直线
,直线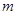 ,
,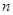 都经过圆C外定点A(1,0).
都经过圆C外定点A(1,0).
(Ⅰ)若直线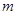 与圆C相切,求直线
与圆C相切,求直线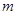 的方程;
的方程;
(Ⅱ)若直线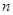 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与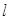 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,
求证: 为定值.
为定值.
(本题满分12分)
已知直线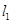 :
: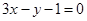 ,
,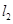 :
: ,求:
,求:
(1)直线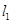 与
与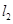 的交点
的交点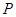 的坐标;(2)过点
的坐标;(2)过点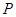 且与
且与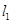 垂直的直线方程.
垂直的直线方程.
(本小题满分12分)
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.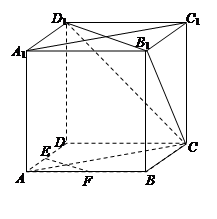
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1
(本小题满分12分)如图,在四边形 中,点C(1,3).
中,点C(1,3).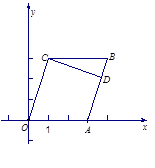
(1)求OC所在直线的斜率;
(2)过点C做CD⊥AB于点D,求CD所在直线的方程.
(满分14分) 定义在 上的函数
上的函数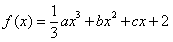 同时满足以下条件:
同时满足以下条件:
①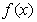 在
在 上是减函数,在
上是减函数,在 上是增函数;②
上是增函数;② 是偶函数;
是偶函数;
③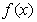 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求函数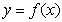 的解析式;
的解析式;
(2)设 ,求函数
,求函数 在
在 上的最小值.
上的最小值.