从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率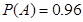 .
.
(Ⅰ) 求从该批产品中任取1件是二等品的概率 ;
;
(Ⅱ) 若该批产品共100件,从中依次抽取2件,求事件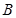 :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率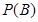 .
.
已知8个球队中有3个弱队,以抽签方式将这8个球队分为A、B两组,每组4个.求
(Ⅰ)A、B两组中有一组恰有两个弱队的概率;
(Ⅱ)A组中至少有两个弱队的概率.
现有7名同学去参加一个活动,分别求出以下不同要求的方法数(以下各小题写出必要的计算公式,最终结果用数字作答)
(1)排队时7名同学中的丙不站在中间的排法
(2)排队时7名同学中的甲、乙、丙三名同学各不相邻的排法
(3)排队时7名同学中的甲不能站在最前并且已不能站在最后的排法(理科学生做)
(4)7名学生选出3名代表发言,甲,乙,丙三名同学至多两人个入选的选法(理科学生做)
7名学生中选出3名代表发言,甲、乙只有一人入选的选法有多少?(文科学生做)
为配合新课程的实施,乌鲁木齐市第一中学联合兄弟学校举行了“应用与创新”知识竞赛,共有1500名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
| 组别 |
分组 |
频数 |
频率 |
| 1 |
49.5~59.5 |
60 |
0.12 |
| 2 |
59.5~69.5 |
120 |
0.24 |
| 3 |
69.5~79.5 |
180 |
0.36 |
| 4 |
79.5~89.5 |
130 |
 |
| 5 |
89.5~99.5 |
 |
0.02 |
| 合计 |
 |
1.00 |
解答下列问题:
(1)在这个问题中,总体是,样本是,
样本容量 =;
=;
(2)第四小组的频率 =;
=;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计此次竞赛获一等奖的人数.
假定乌鲁木齐市第一中学有在编人员160人,其中行政人员16人,教师112人,后勤人员32人。学校为了了解机构改革意见,要从中抽取一个容量为20的样本,请你写出具体的抽样过程。
(本小题共14分)
已知 ,函数
,函数
(1)当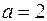 时,求使
时,求使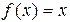 成立的
成立的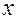 的集合;
的集合;
(2)求函数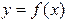 在区间
在区间 上的最小值.
上的最小值.