袋子
和
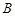中装有若干个均匀的红球和白球，从中摸出一个红球的概率是
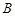，从中摸出一个红球的概率为
．
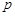（1）从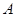
中有放回地摸球，每次摸出一个，共摸4次．
①恰好有2次摸到红球的概率；②第一次、第三次摸到红球的概率．
（2）若、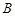两个袋子中的球数之比为4，将、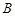中的球装在一起后，从中摸出一个红球的概率是
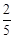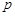，求的值
(本题14分)已知△ABC中，角A，B，C，所对的边分别是a，b，c，且2(a2+b2－c2)=3ab．
(1)求cosC；
(2)若c=2，求△ABC面积的最大值．
(本题14分)已知P(2，1)，直线l：x－y+4=0．
(1)求过点P与直线l平行的直线方程；
(2) 求过点P与直线l垂直的直线方程．
(本大题14分)如图，在棱长为a的正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点．
(1)求证：B1D1∥面EFG
(2)求证：平面AA1C⊥面EFG．
(本题16分)已知{an}是等差数列，且a1=2，a1+a2+a3=12．
(1)求数列{an}的通项公式；
(2)令bn= an3n，求{bn}的前n项的和Tn．
（本小题满分12分）如图所示，四棱锥P—ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=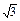
，点F是PB的中点，点E在边BC上移动.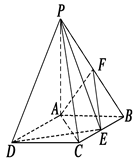
（1）点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（2）求证：无论点E在BC边的何处，都有PE⊥AF；
（3）当BE为何值时，PA与平面PDE所成角的大小为45°.