某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了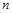 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
| 组号 |
分组 |
回答正确 的人数 |
回答正确的人数 占本组的概率 |
| 第1组 |
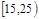 |
5 |
0.5 |
| 第2组 |
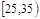 |
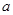 |
0.9 |
| 第3组 |
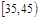 |
27 |
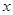 |
| 第4组 |
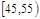 |
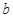 |
0.36 |
| 第5组 |
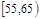 |
3 |
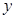 |
(Ⅰ) 分别求出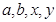 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
在平面直角坐标系中,已知定点A(-2,0)、B(2,0),异于A、B两点的动点P满足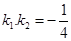 ,其中k1、k2分别表示直线AP、BP的斜率.
,其中k1、k2分别表示直线AP、BP的斜率.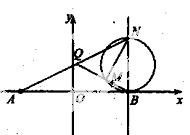
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若N是直线x=2上异于点B的任意一点,直线AN与(I)中轨迹E交予点Q,设直线QB与以NB为直径的圆的一个交点为M(异于点B),点C(1,0),求证:|CM|·|CN|为定值.
某市为准备参加省中学生运动会,对本市甲、乙两个田径队的所有跳高运动员进行了测试,用茎叶图表示出甲、乙两队运动员本次测试的跳高成绩(单位:cm,且均为整数),同时对全体运动员的成绩绘制了频率分布直方图.跳高成绩在185cm以上(包括185cm)定义为“优秀”,由于某些原因,茎叶图中乙队的部分数据丢失,但已知所有运动员中成绩在190cm以上(包括190cm)的只有两个人,且均在甲队. 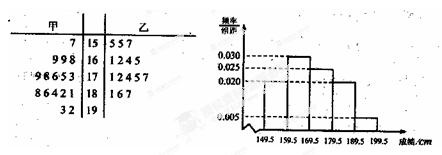
(Ⅰ)求甲、乙两队运动员的总人数a及乙队中成绩在[160,170)(单位:cm)内的运动员人数b;
(Ⅱ)在甲、乙两队所有成绩在180cm以上的运动员中随机选取2人,已知至少有1人成绩为“优秀”,
求两人成绩均“优秀”的概率;
(Ⅲ)在甲、乙两队中所有的成绩为“优秀”的运动员中随机选取2人参加省中学生运动会正式比赛,
求所选取运动员中来自甲队的人数X的分布列及期望.
如图,在直三棱柱 中,
中, ,
, ,异面直线
,异面直线 与
与 所成
所成
的角为 .
.
(Ⅰ)求证: ;
;
(Ⅱ)设 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
设数列{an}是等差数列,数列{bn}的前n项和Sn满足 且
且
(Ⅰ)求数列{an}和{bn}的通项公式:
(Ⅱ)设Tn为数列{Sn}的前n项和,求Tn.
已知无穷数列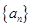 中,
中,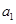 、
、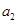 、
、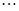 、
、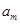 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列,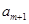 、
、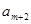 、
、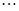 、
、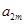 ,构成首项为
,构成首项为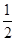 ,公比为
,公比为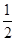 的等比数列,其中
的等比数列,其中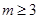 ,
,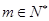 .
.
(1)当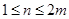 ,
,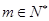 ,时,求数列
,时,求数列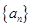 的通项公式;
的通项公式;
(2)若对任意的 ,都有
,都有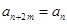 成立.
成立.
①当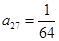 时,求
时,求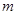 的值;
的值;
②记数列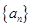 的前
的前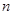 项和为
项和为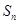 .判断是否存在
.判断是否存在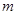 ,使得
,使得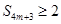 成立?若存在,求出
成立?若存在,求出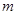 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.