已知无穷数列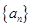 中,
中,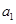 、
、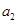 、
、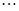 、
、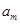 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列,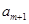 、
、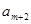 、
、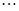 、
、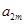 ,构成首项为
,构成首项为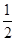 ,公比为
,公比为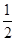 的等比数列,其中
的等比数列,其中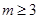 ,
,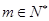 .
.
(1)当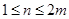 ,
,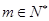 ,时,求数列
,时,求数列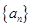 的通项公式;
的通项公式;
(2)若对任意的 ,都有
,都有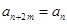 成立.
成立.
①当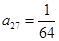 时,求
时,求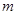 的值;
的值;
②记数列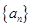 的前
的前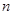 项和为
项和为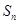 .判断是否存在
.判断是否存在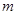 ,使得
,使得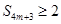 成立?若存在,求出
成立?若存在,求出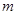 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(理科题)(本小题12分)
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?
(文科题)(本小题12分)
要建造一个无盖长方体水池,底面一边长固定为8m,最大装水量为72m ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2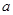 元/
元/ 、
、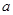 元/
元/ ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
(本小题14分)
在等差数列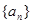 中,
中,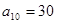 ,
,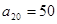 .
.
(1)求数列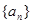 的通项
的通项 ;
;
(2)令 ,证明:数列
,证明:数列 为等比数列;
为等比数列;
(3)求数列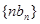 的前
的前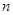 项和
项和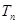 .
.
(本小题12分)
某工厂用两种不同原料可生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可得产品90kg; 若采用乙种原料,每吨成本1500元,运费400元,可得产品100kg,如果每月原料的总成本不超过6000元,运费不超过2000元,那么如何分配甲乙两种原料使此工厂每月生产的产品最多?最多是多少千克?
(本小题12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
(1)求角C的大小;
(2)若c=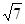 ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值。
,求a+b的值。