(文科题)(本小题12分)
要建造一个无盖长方体水池,底面一边长固定为8m,最大装水量为72m ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2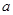 元/
元/ 、
、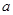 元/
元/ ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
已知函数 .
.
(1)若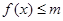 的解集为
的解集为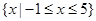 ,求实数
,求实数 的值.
的值.
(2)当 且
且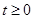 时,解关于
时,解关于 的不等式
的不等式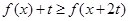 .
.
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.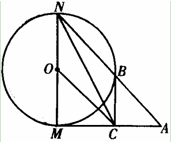
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
已知函数f(x)=alnx+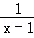 (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若x1∈(0, ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x2)﹣f(x1)≥ln2+
,2]时,求证:f(x2)﹣f(x1)≥ln2+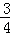 .
.
在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: 的离心率
的离心率 ,且椭圆C上一点
,且椭圆C上一点 到点Q
到点Q 的距离最大值为4,过点
的距离最大值为4,过点 的直线交椭圆
的直线交椭圆 于点
于点
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当 时,求实数
时,求实数 的取值范围.
的取值范围.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.