(理科题)(本小题12分)
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?
如图所示,在△ABC中,点M是BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求AP∶PM的值.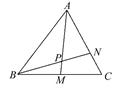
如图,在△ABC中,在AC上取点N,使得AN= AC,在AB上取点M,使得AM=
AC,在AB上取点M,使得AM= AB,在BN的延长线上取点P,使得NP=
AB,在BN的延长线上取点P,使得NP= BN,在CM的延长线上取一点Q,使MQ=λCM时,
BN,在CM的延长线上取一点Q,使MQ=λCM时,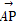 =
=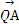 ,试确定λ的值.
,试确定λ的值.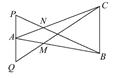
如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按 米处理).
米处理).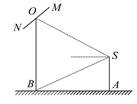
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB.
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角∠MSN(设为θ)是否存在最大值?若存在,请求出∠MSN取最大值时cosθ的值;若不存在,请说明理由.
在海岸A处,发现北偏东45°方向、距离A处(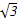 -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10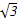 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,向量m=(1,cosB),n=(sinB,- ),且m⊥n.
),且m⊥n.
(1)求角B的大小.
(2)若△ABC的面积为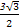 ,a=2,求b的值.
,a=2,求b的值.