如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按 米处理).
米处理).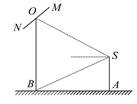
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB.
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角∠MSN(设为θ)是否存在最大值?若存在,请求出∠MSN取最大值时cosθ的值;若不存在,请说明理由.
已知函数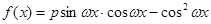
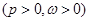 的最大值为
的最大值为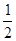 ,小正周期为
,小正周期为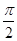 .
.
(Ⅰ)求: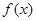 的解析式;
的解析式;
(Ⅱ)若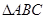 的三条边为
的三条边为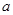 ,
,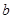 ,
,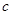 ,满足
,满足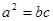 ,
,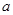 边所对的角为
边所对的角为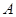 .求角
.求角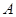 的取值范围及函数
的取值范围及函数 的值域.
的值域.
在区间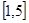 和
和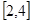 分别各取一个数,记为m和n,求方程
分别各取一个数,记为m和n,求方程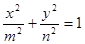 表示焦点在x轴上的椭圆的概率.
表示焦点在x轴上的椭圆的概率.
已知函数
(I)试判断函数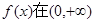 上单调性并证明你的结论;
上单调性并证明你的结论;
(Ⅱ)若 对于
对于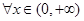 恒成立,求正整数
恒成立,求正整数 的最大值;
的最大值;
(III)求证: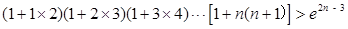
在数列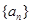 中,
中,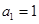 ,
,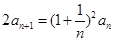
(1)求数列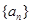 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列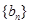 的前
的前 项和
项和
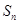 .
.
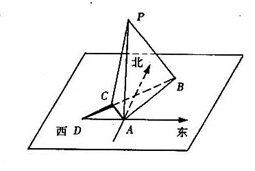
在海岛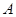 上有一座海拔
上有一座海拔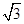 千米的山,山顶设有一个观察站
千米的山,山顶设有一个观察站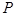 ,上午
,上午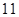 时,测得一轮船在海岛北偏东
时,测得一轮船在海岛北偏东 ,俯角(与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,当目标视线在水平视线的下方时称为俯角)为
,俯角(与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,当目标视线在水平视线的下方时称为俯角)为 的
的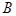 处。到
处。到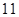 时
时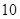 分又测得该轮船在岛西偏北
分又测得该轮船在岛西偏北 ,俯角为
,俯角为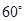 的
的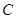 处。
处。
(1)该轮船的航行速度是每小时多少千米?
(2)又经过一段时间后,轮船到达海岛正西方向的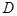 处,此时轮船距岛有多远?
处,此时轮船距岛有多远?