在海岸A处,发现北偏东45°方向、距离A处(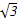 -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10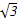 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
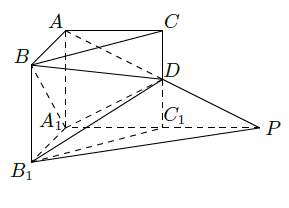
如图,在直三棱柱
中.
,
.
是棱
上的一
是
的延长线与的
延长线的交点,且
平面
.
(I)求证:
:
(II)求二面角
的平面角的余弦值;
(Ⅲ)求点
到平面
的距离.
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为2元(不足1小时的部分按1小时计算).有人独立来该租车点则车骑游.各租一车一次.设甲、乙不超过两小时还车的概率分别为
,
;两小时以上且不超过三小时还车的概率分别为
,
;两人租车时间都不会超过四小时.
(Ⅰ)求出甲、乙所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量
,求
的分布列与数学期望
.
已知函数
(Ⅰ)求
的最小正周期和最小值;
(Ⅱ)已知
,
,求证:
.
已知数列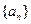 的前
的前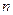 项和为
项和为 ,且
,且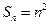 .数列
.数列 为等比数列,且
为等比数列,且 ,
,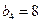 .
.
(Ⅰ)求数列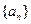 ,
, 的通项公式;
的通项公式;
(Ⅱ)若数列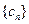 满足
满足 ,求数列
,求数列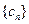 的前
的前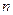 项和
项和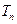 ;
;
已知函数 ,
,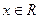
(1)求函数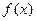 的最小正周期;
的最小正周期;
(2)记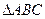 的内角A,B,C的对边长分别为
的内角A,B,C的对边长分别为 ,若
,若 ,求
,求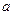 的值。
的值。