某校高一学生1000人,每周一次同时在两个可容纳600人的会议室,开设“音乐欣赏”与“美术鉴赏”的校本课程.要求每个学生都参加,要求第一次听“音乐欣赏”课的人数为
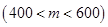 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用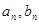 分别表示在第
分别表示在第 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
(1)若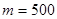 ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
;
(2)①证明数列 是等比数列,并用
是等比数列,并用 表示
表示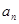 ;
;
②若要求前十次参加“音乐欣赏”课的学生的总人次不超过5800,求 的取值范围.
的取值范围.
(本小题满分12分)已知函数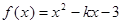 ,
,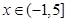 .
.
(Ⅰ)当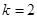 时,求函数
时,求函数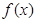 的值域;
的值域;
(Ⅱ)若函数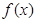 在区间
在区间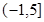 上是单调函数,求实数
上是单调函数,求实数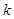 的取值范围.
的取值范围.
(本小题满分12分)已知函数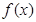 是定义在
是定义在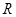 上的偶函数.若
上的偶函数.若 时,
时,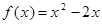 .
.
(Ⅰ)当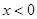 时,求函数
时,求函数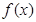 的解析式;
的解析式;
(Ⅱ)画出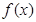 的简图;(要求绘制在答题卷的坐标纸上);
的简图;(要求绘制在答题卷的坐标纸上);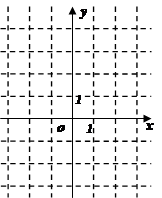
(Ⅲ)结合图像写出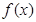 的单调区间(只写结论,不用证明).
的单调区间(只写结论,不用证明).
(本小题满分12分)已知函数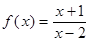 ,其中
,其中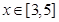 .
.
(Ⅰ)用定义证明函数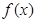 在
在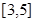 上单调递减;
上单调递减;
(Ⅱ)结合单调性,求函数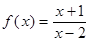 在区间
在区间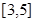 上的最大值和最小值.
上的最大值和最小值.
(本小题满分10分)已知集合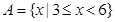 ,
,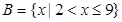 .
.
(Ⅰ)求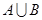 ,
,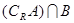 ;
;
(Ⅱ)已知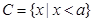 ,若
,若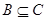 ,求实数
,求实数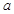 的取值范围.
的取值范围.
(本题满分14分)数列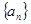 中,
中,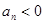 , 前n项和
, 前n项和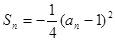 .
.
(1)求数列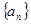 的通项公式;
的通项公式;
(2)设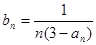 (
(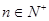 ),
),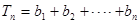 ,若对任意
,若对任意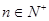 ,总存在
,总存在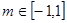 使
使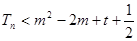 成立,求出t的取值范围.
成立,求出t的取值范围.