有一人患了流感,经过两轮传染后共有64人患了流感.
(1)求每轮传染中平均一个人传染了几个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
如图,两个圈分别表示负数集和分数集. 请你把下列各数填入表示它所在的数集的圈里:
-50%, 2012, 0.618, -3,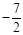 ,0, 5.9,-3.14, -92.
,0, 5.9,-3.14, -92.
如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠1=∠B=∠C.
(1)由题设条件,请写出三个正确结论:(要求不再添加其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)
答:结论一:;结论二:;结论三:.
(2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),
①求CE的最大值;
②若△ADE是等腰三角形,求此时BD的长.(注意:在第(2)的求解过程中,若有运用(1)中得出的结论,须加以证明)
如图,直线 与双曲线
与双曲线 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线 经过点B吗?请说明理由.
经过点B吗?请说明理由.
先阅读理解下列题,再按要求完成问题:
例题:解一元二次不等式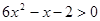
解:把 分解因式得:
分解因式得:
又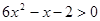 所以
所以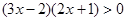 由有理数乘法法则“两数相乘,同号得正”,有
由有理数乘法法则“两数相乘,同号得正”,有
(1) 或(2)
或(2)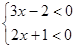 ,解不等式组(1),得
,解不等式组(1),得
解不等式(2),得 因此,一元二次不等式
因此,一元二次不等式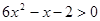 的解集为
的解集为 或
或 ;
;
问题;根据阅读解不等式: .
.
已知关于x的方程 解为正数,求m的取值范围.
解为正数,求m的取值范围.