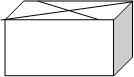
请你设计一个包装盒,如图所示, 是边长为
是边长为 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,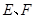 在
在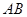 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
.
(1)若广告商要求包装盒侧面积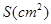 最大,试问
最大,试问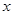 应取何值?
应取何值?
(2)若广告商要求包装盒容积 最大,试问
最大,试问 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.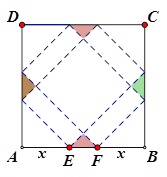
(本小题满分13分)
一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.
(Ⅰ)求取出的3个球颜色相同且编号是三个连续整数的概率;
(Ⅱ)求取出的3个球中恰有2个球编号相同的概率;
(Ⅲ)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.
(本小题满分13分)
已知函数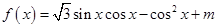
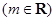 的图象过点
的图象过点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在△ 中,角
中,角 ,
, ,
,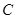 的对边分别是
的对边分别是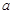 ,
,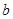 ,
, .若
.若 ,求
,求 的取值范围.
的取值范围.
已知函数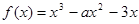 ,
,
(1)若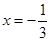 是
是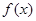 的极值点,求
的极值点,求 值;
值;
(2)若函数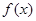 在
在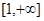 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
斜率为2的直线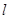 经过抛物线
经过抛物线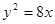 的焦点
的焦点 ,且与抛物线相交于
,且与抛物线相交于 两点,求线段
两点,求线段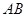 的长。
的长。
已知函数 .
.
(1)求函数的单调区间;
(2)若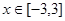 ,试求函数在此区间上的最大值与最小值.
,试求函数在此区间上的最大值与最小值.