如图所示，⊙O内切△ABC的边于D、E、F，AB＝AC，连接AD交⊙O于点H，直线HF交BC的延长线于点G．求证：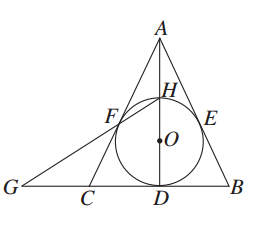
(1)圆心O在直线AD上；
(2)点C是线段GD的中点．
(本小题满分14分)
设三角形
的内角
的对边分别为
,
．
（1）求
边的长；
（2）求角
的大小.
（3）如果
,求
.
如图，已知正三棱柱
的所有棱长都为2，
为棱
的中点，
（1）求证：
平面
；
（2）求二面角
的余弦值大小.
（本题满分10分，选修4-4：极坐标与参数方程）
已知圆C的极坐标方程是
，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线
的参数方程是
（t是参数）。
若直线与圆C相切，求实数m的值.
（本题满分10分，选修4-2：矩阵与变换）
已知二阶矩阵M属于特征值3的一个特征向量为
，并且矩阵M对应的变换将点
变成点
，求出矩阵M.
已知数列
中,
, 
为实常数）,前
项和
恒为正值，且当
时,
.
⑴求证:数列
是等比数列；
⑵设
与
的等差中项为
,比较与
的大小；
⑶设
是给定的正整数，
.现按如下方法构造项数为
有穷数列
：
当
时，
；
当
时，
.
求数列
的前项和
.