在平面直角坐标系中,已知向量点满足,,区域.若为两段分离的曲线,则
已知函数f(x)=2sin ωx在区间上的最小值为-2,则ω的取值范围是
( )
| A.∪[6,+∞) |
| B.∪ |
| C.(-∞,-2]∪[6,+∞) |
| D.∪ |
将函数y=f(x)·sinx的图象向右平移个单位后,再作关于x轴的对称变换得到函数y=1-2sin2x的图象,则f(x)是
( )
| A.-2cosx | B.2cosx |
| C.-2sinx | D.2sinx |
已知=-5,那么tanα的值为
( )
| A.-2 | B.2 |
| C. | D.- |
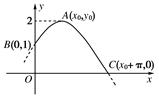
已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为
( )
| A.f(x)=2sin(-) | B.f(x)=cos(4x+) |
| C.f(x)=2cos(-) | D.f(x)=2sin(4x+) |
已知函数f(x)=sin(x+α)cos(x+α),当x=1时,函数f(x)取得最大值,则α的一个取值是
( )
| A. | B. |
| C. | D.π |