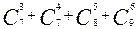某地区2007年至2013年农村居民家庭纯收入(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
| 年份代号 | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 人均纯收入 | 2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(1)求关于的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,
如图,在直三棱柱 ABC- A 1 B 1 C 1中,∠ ACB=90°, AC= BC=CC 1=1,
M为 AB的中点,D为BB 1中点.  (1)求证:平面 CMD⊥平面 ABB 1 A 1;
(1)求证:平面 CMD⊥平面 ABB 1 A 1;
(2)求点 A 1到平面 CMD的距离. 


.(本小题满分12分)高2011级某班"成长共同体"共有男生3人,女生3人.
(1)6个人站成一排,共有多少种站法? 


(2)6个人站成一排,女生不相邻,共有多少种站法?
(3)6个人站成一排合影, 女生必须站在一起的排法总数为多少?
已知 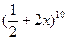 ,求:
,求: 
(1)展开式中的第二项;
(2)展开式中的 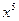 项的系数;
项的系数;
(3)展开式中的二项式系数最大的项. 

如图,在正方体 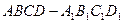 中,
中, 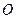 是底面正方形
是底面正方形 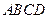 的中心,
的中心, 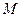 是线段
是线段 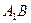 的中点.
的中点. 



(1)证明: 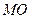 //平面
//平面 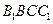 ;
;
(2)异面直线 AC与 A 1D所成的角;
(1)解方程:  ;
; 


(2)求值: