一种水下重物打捞方法的工作原理如图所示。将一质量、体积的重物捆绑在开口朝下的浮筒上。向浮筒内冲入一定质量的气体,开始时筒内液面到水面的距离,筒内气体体积。在拉力作用下浮筒缓慢上升,当筒内液面的距离为时,拉力减为零,此时气体体积为,随后浮筒和重物自动上浮。求和。

已知:大气压强,水的密度,重力加速度的大小。不计水温变化,筒内气体质量不变且可视为理想气体,浮筒质量和筒壁厚度可忽略。
如下图,半径R = 1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h = 0.45m,C点与一倾角为θ = 37°的光滑斜面连接,质量m=1.0 kg的小滑块从圆弧上某点由静止释放,已知滑块与水平面间的动摩擦因数µ=0.1。(已知sin37°=0.6 cos37°="0.8," g取l0 m/s2)求:
(1)若小滑块到达圆弧B点时对圆弧的压力刚好等于其重力的2倍,则小滑块应从圆弧上离地面多高处释放;
(2)若在C点放置一个质量M=2.0kg的小球,小滑块运动到C点与小球正碰后返回恰好停在B点,求小滑块与小球碰后瞬间小滑块的速度大小。
(3)小滑块与小球碰后小球将落在何处并求其在空中的飞行时间。
如图所示,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与R=0.24m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以v0=6m/s的初速度滑上小车左端,二者共速时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2,求: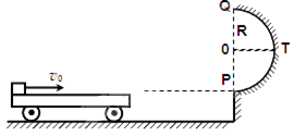
(1)滑块与小车共速时的速度及小车的最小长度;
(2)滑块m恰好从Q点离开圆弧轨道时小车的长度;
(3)讨论小车的长度L在什么范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道?
如图所示,坡道顶端距水平面高度为h,质量为m1的小物块A从坡道顶端由静止滑下,进入水平面上的滑道时无机械能损失,为使A制动,将轻弹簧的一端固定在水平滑道延长线M处的墙上,另一端与质量为m2的挡板B相连,弹簧处于原长时,B恰位于滑道的末端O点。A与B碰撞时间极短,碰后结合在一起共同压缩弹簧,已知在OM段A、B与水平面间的动摩擦因数均为μ,其余各处的摩擦不计,重力加速度为g,求
(1)物块A在与挡板B碰撞前瞬间速度v的大小;
(2)弹簧最大压缩量为d时的弹性势能EP(设弹簧处于原长时弹性势能为零)。
如甲图所示,水平光滑地面上用两颗钉子(质量忽略不计)固定停放着一辆质量为M=3kg的小车,小车的四分之一圆弧轨道是光滑的,半径为R=0.5m,在最低点B与水平轨道BC相切,视为质点的质量为m=1kg的物块从A点正上方距A点高为h=0.3m处无初速下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行恰好停在轨道末端C。
现去掉钉子(水平面依然光滑未被破坏)不固定小车,而让其左侧靠在竖直墙壁上,该物块仍从原高度处无初速下落,如乙图所示。
不考虑空气阻力和物块落入圆弧轨道时的能量损失,已知物块与水平轨道BC间的动摩擦因数为μ=0.2
求:(1)水平轨道BC长度;
(2)小车固定时物块到达圆弧轨道最低点B时对轨道的压力;
(3)小车不固定时物块再次停在小车上时距小车B点的距离;
(4)两种情况下由于摩擦系统产生的热量之比。
如图所示,在光滑的水平地面上,静止着质量为M =2.0kg的小车A,小车的上表面距离地面的高度为0.8m,小车A的左端叠放着一个质量为m=1.0kg的小物块B(可视为质点)处于静止状态,小物块与小车上表面之间的动摩擦因数μ=0.20。在小车A的左端正上方,用长为R=1.6m的不可伸长的轻绳将质量为m =1.0kg的小球C悬于固定点O点。现将小球C拉至使轻绳拉直且与竖起方向成θ=60°角的位置由静止释放,到达O点的正下方时,小球C与B发生弹性正碰(碰撞中无机械能损失),小物块从小车右端离开时车的速度为1m/s,空气阻力不计,取g=10m/s2. 求:
(1)小车上表面的长度L是多少?
(2)小物块落地时距小车右端的水平距离是多少?