一竖直悬挂的弹簧振子,下端装有一记录笔,在竖直面内放置有一记录纸,当振子上下振动时,以速率水平向左匀速拉动记录纸,记录笔在纸上留下如图所示的图像.、、、为纸上印迹的位置坐标,由此图求振动的周期和振幅.

如图所示, 有A、B、C三个小球,A距地面较高,B其次,C最低,A、C两球相距10m,并且在同一竖直平面上,三球同时开始运动,C作竖直上抛,B作平抛,A作竖直下抛,三个球初速度相同,5s后三个球相遇,不计空气阻力,求:
(1)三个球的初速度各多大?
(2)开始运动时,B球与C球的水平距离和竖直距离各是多少?
把带电荷量2×10-8 C的正点电荷从无限远处移到电场中A点,要克服电场力做功8×10-6 J,若把该电荷从无限远处移到电场中B点,需克服电场力做功2×10-6 J,求:
(1)A点的电势;
(2)A、B两点的电势差;
(3)把2×10-5 C的负电荷由A点移到B点电场力做的功.
一辆汽车质量为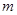 ,从静止开始起动,沿水平面前进了
,从静止开始起动,沿水平面前进了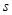 米后,就达到了最大行驶速度
米后,就达到了最大行驶速度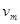 ,设汽车的牵引功率保持不变,所受阻力为车重的
,设汽车的牵引功率保持不变,所受阻力为车重的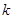 倍。求:
倍。求:
(1)汽车的牵引力功率。
(2)汽车从静止到开始匀速运动所需的时间(提示:汽车以额定功率起动后的运动不是匀加速运动)。
处于静止状态的某原子核X,发生α衰变后变成质量为M的原子核Y,被释放的α粒子垂直射人磁感强度为B的匀强磁场中,测得其圆周运动的半径为r,设α粒子质量为m,质子的电量为e,试求: (提示:原子核衰变过程中,动量和能量保持守恒)
(1)衰变后α粒子的速率υa和动能Eka;
(2)衰变后Y核的速率υy和动能Eky;
(3)衰变前X核的质量Mx.
如图,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度E=10 N/C;在x<0的空间中存在垂直于xOy平面方向的匀强磁场,磁感应强度B=0.5 T。一带负电的粒子(比荷q/m=160 C/kg),在x=0.06 m处的D点以v0=8 m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力。求: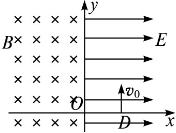
(1)带电粒子开始运动后第一次通过y轴时距O点的距离。
(2)带电粒子开始运动后第一次通过y轴的速度大小和方向;
(3)带电粒子进入磁场后经多长时间返回电场;