已知两条直线m,n,两个平面α,β.给出下面四个命题:
①m∥n,m⊥α⇒n⊥α;
②α∥β,m⊂α,n⊂β⇒m∥n;
③m∥n,m∥α⇒n∥α;
④α∥β,m∥n,m⊥α⇒n⊥β.
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是()
| A.72 | B.96 | C.108 | D.144 |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
| A.-1<a<2 | B.-3<a<6 | C.a<-1或a>2 | D.a<-3或a>6 |
已知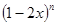 的展开式中,奇数项的二项式系数之和是64,则
的展开式中,奇数项的二项式系数之和是64,则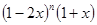 的展开式中,
的展开式中, 的系数是()
的系数是()
| A.280 | B.-280 | C.-672 | D.672 |
给出定义:若函数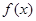 在D上可导,即
在D上可导,即 存在,且导函数
存在,且导函数 在D上也可导,则称
在D上也可导,则称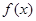 在D上存在二阶导函数,记
在D上存在二阶导函数,记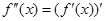 ,若
,若 > 0在D上恒成立,则称
> 0在D上恒成立,则称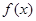 在D上为凹函数,以下四个函数在
在D上为凹函数,以下四个函数在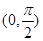 上是凹函数的是( )
上是凹函数的是( )
A.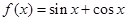 |
B. |
C.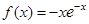 |
D.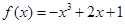 |
设 ,函数
,函数 的导函数是
的导函数是 ,且
,且 是奇函数,若曲线
是奇函数,若曲线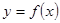 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为()
,则切点的横坐标为()
A.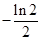 |
B.-ln2 | C.ln2 | D.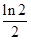 |