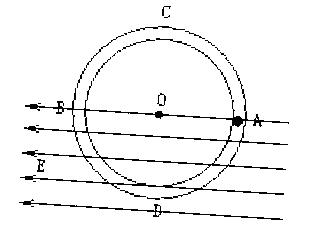
为了研究过山车的原理,某兴趣小组提出了下列设想:取一个与水平方向夹角为37°、长为l = 2.0m的粗糙倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s从某一高处水平抛出,到A点时速度方向恰好沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数 μ = 0.50.(g=10m/s2、sin37°= 0.60、cos37° =0.80)
⑴求小物块到达A点时速度。
⑵要使小物块不离开轨道,并从轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件?
⑶为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则竖直圆轨道的半径应该满足什么条件?
如图所示,一个质量为 的垒球,以
的垒球,以 的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为
的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为 ,设球棒与垒球的作用时间为
,设球棒与垒球的作用时间为 。求:
。求:球棒对垒球的平均作用力大小;
球棒对垒球做的功

如图,半径为R的环形塑料管固定在竖直面放置,AB为管的水平直径,管的粗细远小于管的半径,AB及其以下部分处于水平向左的匀强电场中,管的内壁光滑,现将一质量为m、带正电小球从管中A点静止释放,已知小球受到的重力与它受到的电场力相等,重力加速度为g,则释放后:求小球第一次经过最低点D时的速率;
小球第二次经过最高点C时,管壁对小球的作用力?
下图甲是一种家用电熨斗的电路原理图(额定电压为220 V).R0是定值电阻,R是可变电阻(调温开关),其电阻值均不受温度影响.
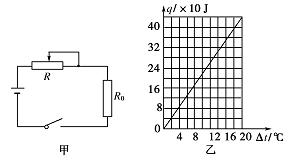
该电熨斗温度最低时的耗电功率为121 W,温度最高时的耗电功率为484 W,求R0的阻值及R的阻值变化范围.
假定电熨斗每秒钟散发的热量q跟电熨斗表面温度与环境温度的温差关系如图乙所示,现在温度为20 ℃的房间使用该电熨斗来熨烫毛料西服,要求熨斗表面温度为220 ℃,且保持不变,问应将R的阻值调为多大?
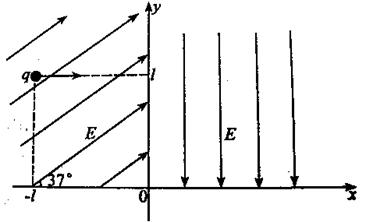
如图xoy平面坐标系,x轴方向为水平方向,y轴方向为竖直方向,在第一象限内有竖直向下的匀强电场E,在第二象限内场强为E的匀强电场与x轴正方向成37°(sin37°="0.6," cos37°=0.8),在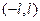 处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求:
处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求:带电小球第一次经过x轴时的位置坐标
带电小球第一次经过x轴是的动能
如图所示为粮食仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距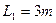 ;另一台倾斜传送,传送带与地面间的倾角
;另一台倾斜传送,传送带与地面间的倾角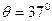 ,C、D两端相距
,C、D两端相距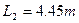 ,B、C相距很近。水平传送带以
,B、C相距很近。水平传送带以 沿顺时针方向转动。现将质量为
沿顺时针方向转动。现将质量为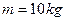 的一袋大米无初速度的放在A端,它随传送带到达B点后,速度大小不变的传到倾斜传送带的C端。米袋与两传送带之间的动摩擦因素均为
的一袋大米无初速度的放在A端,它随传送带到达B点后,速度大小不变的传到倾斜传送带的C端。米袋与两传送带之间的动摩擦因素均为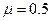 ,取
,取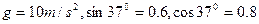
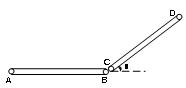
若倾斜传送带CD不转动,则米袋沿传送带CD所能上滑的最大距离是多少?
若倾斜传送带CD以
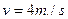 的速率沿顺时针方向转动,则米袋从C端运动到D端的时间为多少?
的速率沿顺时针方向转动,则米袋从C端运动到D端的时间为多少?