已知椭圆的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆的标准方程;
(2)设为椭圆的左焦点,为直线上任意一点,过作的垂线交椭圆于点.
(i)证明:平分线段(其中为坐标原点);
(ii)当最小时,求点的坐标.
已知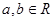 ,
,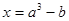 ,
,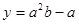 ,试比较
,试比较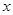 与
与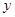 的大小.
的大小.
在平面直角坐标系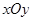 中,已知椭圆
中,已知椭圆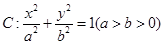 的左焦点为
的左焦点为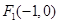 ,且椭圆
,且椭圆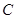 的离心率
的离心率 .
.
(1)求椭圆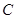 的方程;
的方程;
(2)设椭圆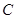 的上下顶点分别为
的上下顶点分别为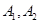 ,
,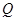 是椭圆
是椭圆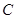 上异于
上异于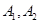 的任一点,直线
的任一点,直线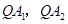 分别交
分别交 轴于点
轴于点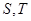 ,证明:
,证明: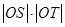 为定值,并求出该定值;
为定值,并求出该定值;
(3)在椭圆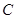 上,是否存在点
上,是否存在点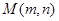 ,使得直线
,使得直线 与圆
与圆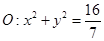 相交于不同的两点
相交于不同的两点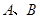 ,且
,且 的面积最大?若存在,求出点
的面积最大?若存在,求出点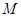 的坐标及对应的
的坐标及对应的 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
如图,四面体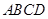 中,
中,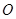 、
、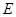 分别是
分别是 、
、 的中点,
的中点,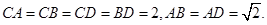
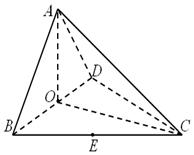
(Ⅰ)求证: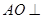 平面
平面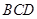 ;
;
(Ⅱ)求二面角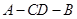 的正切值;
的正切值;
(Ⅲ)求点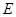 到平面
到平面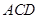 的距离.
的距离.
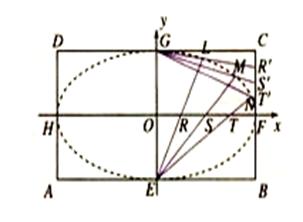
矩形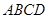 的中心在坐标原点,边
的中心在坐标原点,边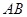 与
与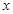 轴平行,
轴平行,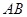 =8,
=8, =6.
=6.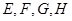 分别是矩形四条边的中点,
分别是矩形四条边的中点,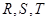 是线段
是线段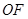 的四等分点,
的四等分点,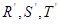 是线段
是线段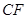 的四等分点.设直线
的四等分点.设直线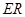 与
与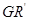 ,
,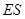 与
与 ,
,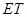 与
与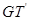 的交点依次为
的交点依次为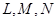 .
.
(1)以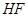 为长轴,以
为长轴,以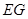 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点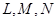 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段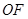 的
的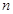 (
(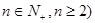 等分点从左向右依次为
等分点从左向右依次为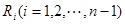 ,线段
,线段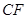 的
的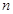 等分点从上向下依次为
等分点从上向下依次为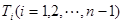 ,那么直线
,那么直线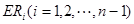 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
已知数列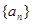 的前
的前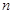 项的和为
项的和为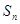 ,
,  ,求证:数列
,求证:数列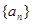 为等差数列的充要条件是
为等差数列的充要条件是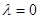 .
.