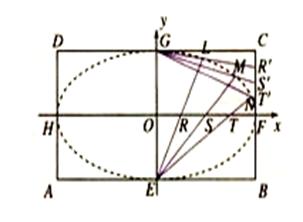
矩形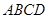 的中心在坐标原点,边
的中心在坐标原点,边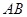 与
与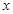 轴平行,
轴平行,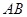 =8,
=8, =6.
=6.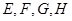 分别是矩形四条边的中点,
分别是矩形四条边的中点,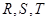 是线段
是线段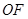 的四等分点,
的四等分点,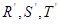 是线段
是线段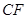 的四等分点.设直线
的四等分点.设直线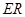 与
与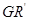 ,
,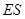 与
与 ,
,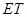 与
与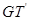 的交点依次为
的交点依次为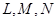 .
.
(1)以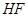 为长轴,以
为长轴,以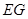 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点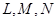 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段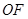 的
的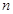 (
(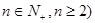 等分点从左向右依次为
等分点从左向右依次为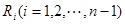 ,线段
,线段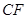 的
的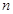 等分点从上向下依次为
等分点从上向下依次为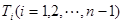 ,那么直线
,那么直线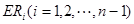 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
如图,ABCD是块矩形硬纸板,其中AB=2AD,AD= ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.
(1)求证:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1= .
.
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA= ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
已知数列{an}的前n项和为Sn,且满足Sn=n2,数列{bn}满足bn= ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.
(1)求数列{an}的通项公式an和Tn;
(2)若对任意的n∈N*,不等式λTn<n+(-1)n恒成立,求实数λ的取值范围.