(Ⅰ)若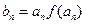 ,记数列
,记数列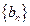 的前n项和为
的前n项和为 ,当
,当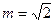 时,求
时,求 ;
;
(Ⅱ)若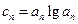 ,问是否存在实数
,问是否存在实数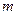 ,使得
,使得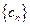 中每一项恒小于它后面的项?若存
中每一项恒小于它后面的项?若存
在,求出实数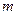 的取值范围
的取值范围
(Ⅰ)当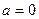 时,求
时,求 的极值;
的极值;
(Ⅱ)若 在区间
在区间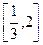 上是增函数,求实数
上是增函数,求实数 的取值范围
的取值范围
(1)平面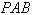 是否垂直于平面
是否垂直于平面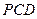 ?
?
(2)求三棱锥 的体积.
的体积.
设M是由满足下列条件的函数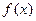 构成的集合:“①方程
构成的集合:“①方程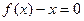 有实数根;②函数
有实数根;②函数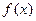 的导数
的导数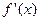 满足
满足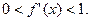 ”
”
(I)证明:函数 是集合M中的元素;
是集合M中的元素;
(II)证明:函数 具有下面的性质:对于任意
具有下面的性质:对于任意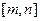
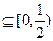 ,都存在
,都存在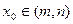 ,使得等式
,使得等式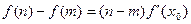 成立。
成立。
(III)若集合M中的元素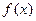 具有下面的性质:若
具有下面的性质:若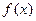 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]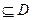 ,都存在
,都存在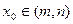 ,使得等式
,使得等式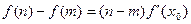 成立。试用这一性质证明:对集合M中的任一元素
成立。试用这一性质证明:对集合M中的任一元素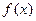 ,方程
,方程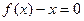 只有一个实数根。
只有一个实数根。
抛物线的顶点在原点,焦点在射线x-y+1=0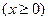 上
上
(1)求抛物线的标准方程
(2)过(1)中抛物线的焦点F作动弦AB,过A、B两点分别作抛物线的切线,设其交点为M,求点M的轨迹方程,并求出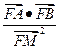 的值
的值