已知抛物线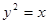 的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
已知双曲线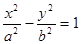 的离心率
的离心率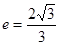 ,过
,过 的直线到原点的距离是
的直线到原点的距离是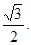
(1)求双曲线的方程;
(2)已知直线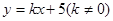 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
已知抛物线y2=8x上两个动点A、B及一个定点M(x0, y0),F是抛物线的焦点,且|AF|、|MF|、|BF|成等差数列,线段AB的垂直平分线与x轴交于一点N.
(1)求点N的坐标(用x0表示);
(2)过点N与MN垂直的直线交抛物线于P、Q两点,若|MN|=4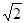 ,求△MPQ的面积.
,求△MPQ的面积.
(本小题满分12分)在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(1)求曲线C1的方程;
(2)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于
点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
(本小题满分12分)已知顶点在坐标原点,焦点在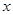 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点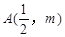 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设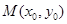 为抛物线上的一个定点,过
为抛物线上的一个定点,过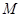 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦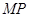 ,
,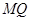 ,求证:
,求证: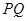 恒过定点
恒过定点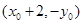 .(3)直线
.(3)直线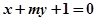 与抛物线交于
与抛物线交于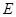 ,
,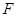 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点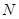 ,使得△
,使得△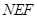 为以
为以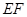 为斜边的直角三角形.
为斜边的直角三角形.