甲袋中有3个白球和4个黑球,乙袋中有5个白球和4个黑球,现在从甲、乙两袋中各取出2个球。(I)求取得的4个球均是白球的概率;(II)求取得白球个数 的数学期望
的数学期望
(本小题满分12分)
已知函数 (
( ,实数
,实数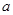 ,
, 为常数).
为常数).
(Ⅰ)若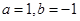 ,求
,求 在
在 处的切线方程;
处的切线方程;
(Ⅱ)若 ,讨论函数
,讨论函数 的单调性.
的单调性.
(本小题满分12分)
为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
| 队别 |
北京 |
上海 |
天津 |
八一 |
| 人数 |
4 |
6 |
3 |
5 |
(Ⅰ)从这18名队员中随机选出两名,求两人来自同一支队的概率;
(Ⅱ)中国女排奋力拼搏,战胜韩国队获得冠军.若要求选出两位队员代表发言,设其中来自北京队的人数为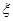 ,求随机变量
,求随机变量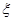 的分布列,及数学期望
的分布列,及数学期望 .
.
(本小题满分12分)
如图,四棱锥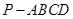 的底面为正方形,侧棱
的底面为正方形,侧棱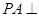 底面
底面 ,且
,且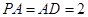 ,
, 分别是线段
分别是线段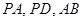 的中点.
的中点.
(Ⅰ)求证: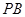 //平面
//平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
(本小题满分10分)
在 中,
中, 分别为角
分别为角 所对的三边,已知
所对的三边,已知 .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若 ,
, ,求
,求 的长.
的长.
(本小题满分14分)
已知函数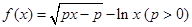 .
.
(Ⅰ)若函数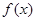 在定义域内为增函数,求实数
在定义域内为增函数,求实数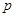 的取值范围;
的取值范围;
(Ⅱ)当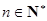 时,试判断
时,试判断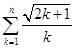 与
与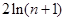 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
(Ⅲ) 当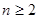 且
且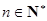 时,证明:
时,证明: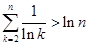 .
.