如图,某小区准备绿化一块直径为 的半圆形空地,
的半圆形空地,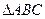 外的地方种草,
外的地方种草,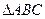 的内接正方形
的内接正方形 为一水池,其余地方种花.若
为一水池,其余地方种花.若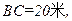
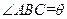 ,设
,设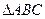 的面积为
的面积为 ,正方形
,正方形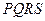 的面积为
的面积为 ,将比值
,将比值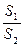 称为“规划合理度”.
称为“规划合理度”.

(1)试用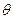 表示
表示 和
和 .(2)当
.(2)当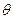 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角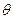 的大小.
的大小.
某单位实行休年假制度三年来,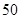 名职工休年假的次数进行的调查统计结果如下表所示:
名职工休年假的次数进行的调查统计结果如下表所示:
| 休假次数 |
 |
 |
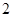 |
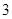 |
| 人数 |
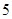 |
 |
 |
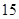 |
根据上表信息解答以下问题:
⑴从该单位任选两名职工,用 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数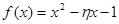 ,在区间
,在区间 ,
,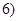 上有且只有一个零点”为事件
上有且只有一个零点”为事件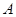 ,求事件
,求事件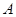 发生的概率
发生的概率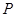 ;
;
⑵从该单位任选两名职工,用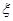 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量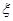 的分布列及数学期望
的分布列及数学期望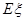 .
.
已知函数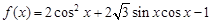
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)在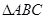 中,角
中,角 所对的边分别是
所对的边分别是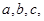 若
若 且
且 ,试判断
,试判断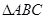 的形状.
的形状.
已知函数
.
(Ⅰ)求
的单调区间;
(Ⅱ)证明:当
时,
.
已知
分别是椭圆
的左、右焦点
关于直线
的对称点是圆
的一条直径的两个端点.
(Ⅰ)求圆
的方程;
(Ⅱ)设过点
的直线
被椭圆
和圆
所截得的弦长分别为
.当
最大时,求直线
的方程.
设
为数列{
}的前项和,已知
,2
(Ⅰ)求
,
,并求数列{
}的通项公式;
(Ⅱ)求数列{
}的前
项和。