(13分)有一批电脑原价2000元,甲、乙两个商店均有销售,甲商店按如下方法促销:在10台内(不含10台)买一台优惠2.5%,买两台优惠5%,买三台优惠7.5%……,依此类推,即多买一台,每台再优惠2.5个百分点(1%叫做一个百分点),10台后(含10台)每台1500元;乙商店一律原价的80%销售。某学校要买一批电脑,去哪家商店购买更合算?
(12分)
已知实数x满足不等式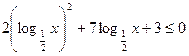
⑴ 求x的取值范围;
⑵ 在⑴的条件下,求函数 的最大值和最小值。
的最大值和最小值。
(12分) 设函数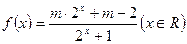 是奇函数。
是奇函数。
⑴ 求实数m的值;
⑵ 若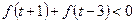 ,求实数t的取值范围。
,求实数t的取值范围。
(12分) 已知函数
⑴ 若 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。
⑵ 求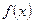 在区间
在区间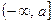 上的最小值
上的最小值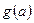 的表达式。
的表达式。
(12分) 设集合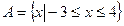 ,
,
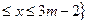 ,若
,若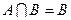 ,求实数m的取值范围。
,求实数m的取值范围。