设M是由满足下列条件的函数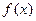 构成的集合:“①方程
构成的集合:“①方程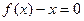 有实数根;②函数
有实数根;②函数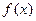 的导数
的导数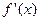 满足
满足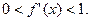 ”
”
(I)证明:函数 是集合M中的元素;
是集合M中的元素;
(II)证明:函数 具有下面的性质:对于任意
具有下面的性质:对于任意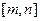
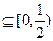 ,都存在
,都存在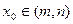 ,使得等式
,使得等式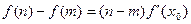 成立。
成立。
(III)若集合M中的元素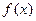 具有下面的性质:若
具有下面的性质:若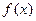 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]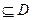 ,都存在
,都存在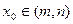 ,使得等式
,使得等式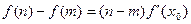 成立。试用这一性质证明:对集合M中的任一元素
成立。试用这一性质证明:对集合M中的任一元素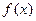 ,方程
,方程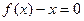 只有一个实数根。
只有一个实数根。
(文)已知半径为5的圆的圆心在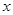 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线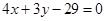 相切.
相切.
(1)求圆的标准方程;
(2)设直线
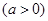 与圆相交于
与圆相交于 两点,求实数
两点,求实数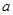 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数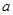 ,使得弦
,使得弦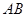 的垂直平分线
的垂直平分线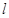 过点
过点 ,
,
如图,在四面体 中,
中, ,
,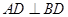 ,点
,点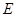 ,
,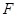 分别是
分别是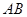 ,
, 的中点.
的中点.
(1)EF∥平面ACD;
(2)求证:平面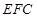 ⊥平面
⊥平面 ;
;
(3)若平面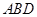 ⊥平面
⊥平面 ,且
,且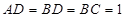 ,求三棱锥
,求三棱锥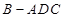 的体积.
的体积.
已知圆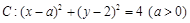 及直线
及直线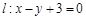 . 当直线
. 当直线 被圆
被圆 截得的弦长为
截得的弦长为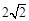 时, 求(1)
时, 求(1) 的值;(2)求过点
的值;(2)求过点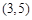 并与圆
并与圆 相切的切线方程.
相切的切线方程.
已知直线经过点 ,求分别满足下列条件的直线方程:
,求分别满足下列条件的直线方程:
(1)倾斜角的正弦为 ;
;
(2)与两坐标轴的正半轴围成的三角形面积为4.
设函数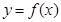 的定义域为
的定义域为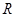 ,并且满足
,并且满足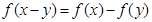 ,且
,且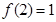 ,当
,当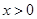 时,
时,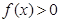
(1).求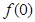 的值;
的值;
(2).判断函数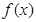 的奇偶性;
的奇偶性;
(3).如果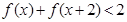 ,求
,求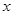 的取值范围.
的取值范围.