(本小题满分12分)广东某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取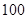 名学生的成绩,按成绩分组:第
名学生的成绩,按成绩分组:第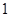 组
组 ,第
,第 组
组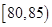 ,第
,第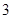 组
组 ,第
,第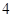 组
组 ,第
,第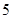 组
组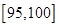 得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第
得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第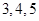 组中用分层抽样抽取
组中用分层抽样抽取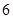 名学生进入第二轮面试.
名学生进入第二轮面试.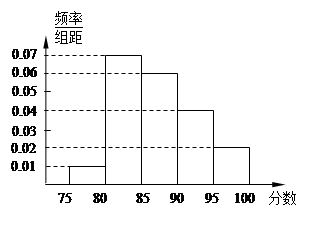
(1)求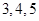 组各应该抽取多少人进入第二轮面试;
组各应该抽取多少人进入第二轮面试;
(2)学校决定在(1)中抽取的这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有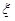 名学生被考官D面试,求
名学生被考官D面试,求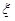 的分布列和数学期望.
的分布列和数学期望.
下表给出甲、乙、丙三种食物的维生素A、B的含量及成本,营养师想购这三种食物共10千克,使之所含维生素A不少于4 400单位,维生素B不少于4 800单位.
| 甲 |
乙 |
丙 |
|
| 维生素A(单位/千克) |
400 |
600 |
400 |
| 维生素B(单位/千克) |
800 |
200 |
400 |
| 成本(元/千克) |
7 |
6 |
5 |
(1)试用所购甲、乙两种食物的量表示成本;
(2)三种食物各购多少时,成本最低?最低成本是多少?
已知实系数方程x2+ax+2b=0的两根在(0,1)与(1,2)内,求 的取值范围.
的取值范围.
如下图所示,求△PQR内任一点(x,y)满足的关系式.
求z=3x+5y的最大值和最小值,使式中的x、y满足约束条件
已知 、
、 是两个不共线的向量,若它们起点相同,
是两个不共线的向量,若它们起点相同, 、
、
 、t(
、t( +
+ )三向量的终点在一直线上,则实数t=_________.
)三向量的终点在一直线上,则实数t=_________.