下表给出甲、乙、丙三种食物的维生素A、B的含量及成本,营养师-优题课

题文

下表给出甲、乙、丙三种食物的维生素A、B的含量及成本,营养师想购这三种食物共10千克,使之所含维生素A不少于4 400单位,维生素B不少于4 800单位.

(1)试用所购甲、乙两种食物的量表示成本;
(2)三种食物各购多少时,成本最低?最低成本是多少?

科目数学题型解答题难度较易

相关试题

已知各项均为正数的数列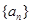满足，且，其中.
（Ⅰ）求数列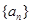的通项公式；
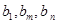（Ⅱ）设数列满足是否存在正整数m、n（1<m<n），使得成等比数列？若存在，求出所有的m、n的值，若不存在，请说明理由。

如图，在四棱锥P—ABCD中，ABCD为平行四边形，且BC⊥平面PAB，PA⊥AB，M为PB的中点，PA=AD=2.

（Ⅰ）求证：PD//平面AMC；
（Ⅱ）若AB=1，求二面角B—AC—M的余弦值。

已知函数.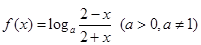
（Ⅰ）当a=3时，求函数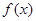在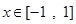上的最大值和最小值；
（Ⅱ）求函数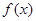的定义域，并求函数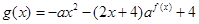的值域。（用a表示）

函数.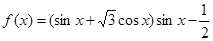
（Ⅰ）求函数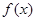的单调递减区间；
（Ⅱ）将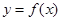的图像向左平移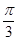个单位，再将得到的图像横坐标变为原来的2倍（纵坐标不变）后得到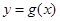的图像，若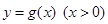的图像与直线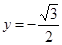交点的横坐标由小到大依次是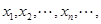求数列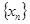的前2n项的和。

如图，平面四边形ABCD中，AB=13，AC=10， AD=5，，.

（Ⅰ）；
（Ⅱ）设，求x、y的值。