设M={x|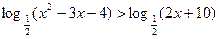 },
},
N={x|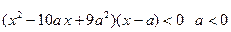 },求M∩N≠
},求M∩N≠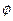 时a的取值范围.
时a的取值范围.
已知定点A(0,1),B(0,-1),C(1,0).动点P满足: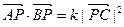 .
.
(I)求动点P的轨迹方程,并说明方程表示的曲线类型;
(II)当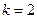 时,求
时,求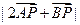 的最大、最小值.
的最大、最小值.
已知气象台A处向西300km处,有个台风中心,已知台风以每小时40km的速度向东北方向移动,距台风中心250km以内的地方都处在台风圈内,问:从现在起,大约多长时间后,气象台A处进入台风圈?气象台A处在台风圈内的时间大约多长?(精确到0.1)(提供参考数据: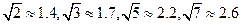 )
)
(10分)已知直线l:kx-y+1+2k=0.
(1)求证:直线l恒过某个定点;
(2)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S,求S的最小值并求此时直线l的方程;
预算用2000元购买单件为50元的桌子和20元的椅子,希望使桌椅的总数尽可能的多,但椅子不少于桌子数,且不多于桌子数的1
 5倍,问桌、椅各买多少才行?
5倍,问桌、椅各买多少才行?