已知函数f (t)=log2(2-t)+ 的定义域为D.
的定义域为D.
(1)求D;
(2)若函数g (x)=x2+2mx-m2在D上存在最小值2,求实数m的值.
求下列各函数的导数。
(1)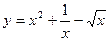 (2)
(2)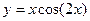
(本题满分14分).有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体形无盖容器(切、焊损耗忽略不计).有人应用数学知识作如下设计:在钢板的四个角处各切去一个边长为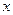
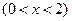 的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.
的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.
(1)请你求出这种切割、焊接而成的长方体容器的的容积V1(用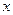 表示);
表示);
(2)经过设计(1)的方法,计算得到当 时,Vl取最大值
时,Vl取最大值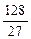 ,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。
,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。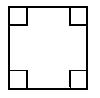
(本题满分14分).如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,
∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=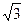 .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD于H点,判定H点位于平面ABCD的那个具体位置?(无须证明)
(Ⅲ)求二面角A-BE-P的大小. 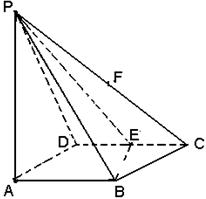
(本题满分14分).如图,圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上的一点,如果QB的中点为C,OH⊥SC,垂足为H。
求证:BQ⊥平面SOC,
求证:OH⊥平面SBQ;设 ,
, ,求此圆锥的体积。
,求此圆锥的体积。
(本题满分14分).如图,在棱长为4的正方体ABCD-A1B1C1D1中,E是D1C1上的一点且EC1=3D1 E,
(1) 求直线BE与平面ABCD所成角的正切值;
(2)求异面直线BE与CD所成角的余弦值.