若函数 在区间
在区间 上的最大值为
上的最大值为 ,求实数
,求实数 的值.
的值.
在△ABC中,已知B(-2,0)、C(2,0),AD⊥BC于点D,△ABC的垂心为H,且 =
=
 .
.
(1)求点H(x,y)的轨迹G的方程;
(2)已知P(-1,0)、Q(1,0),M是曲线G上的一点,那么 ,
, ,
, 能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
如下图,双曲线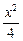 -
-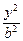 =1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.
=1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.
求以椭圆 +
+ =1的顶点为焦点,且一条渐近线的倾斜角为
=1的顶点为焦点,且一条渐近线的倾斜角为 的双曲线方程.
的双曲线方程.
已知椭圆 +
+ =1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.
=1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.