已知数列{an}是等差数列，数列{bn}是等比数列，且对任意的n∈N*，都有a1b1＋a2b2＋a3b3＋···＋anbn＝n·2n+3．
（1）若{bn}的首项为4，公比为2，求数列{an＋bn}的前n项和Sn；
（2）若a1＝8．
①求数列{an}与{bn}的通项公式；
②试探究：数列{bn}中是否存在某一项，它可以表示为该数列中其它r（r∈N，r≥2）项的和？若存在，请求出该项；若不存在，请说明理由．
（本小题满分14分）已知函数f（x）=ax+
（a＞1）．
（1）判定函数f（x）在（－1，+∞）上的单调性，并给出证明；
（2）证明方程f（x）=0没有负数根．
（本小题满分14分）已知函数f(x)＝a2x＋2ax－1(a>0，且a≠1)在区间[－1,1]上的最大值为14，求实数a的值．
(本小题满分14分) 函数f(x)的图象是如下图所示的折线段OAB，点A的坐标为(1,2)，点B的坐标为(3,0)．
（1）求f(x)的解析式
（2）定义函数g(x)＝f(x)·(x－1)，求函数g(x)的最大值。
（本小题满分12分）已知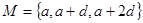
，
，
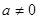，M=N,求q的值
（本小题满分12分）定义A⊗B＝{z|z＝xy＋
，x∈A，y∈B}．设集合A＝{0,2}，B＝{1,2}
1．求集合A⊗B的所有元素之和． 2．写出集合A⊗B的所有真子集。