已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0,且直线l与圆C交于A、B两点.
(1)若|AB|=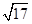 ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P(1,1)满足2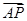 =
=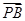 ,求此时直线l的方程.
,求此时直线l的方程.
(本小题满分13分)如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量, ,
,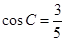 .
.
(Ⅰ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅱ)为使两位游客在 处互相等待的时间不超过
处互相等待的时间不超过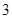 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?
已知函数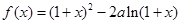
 .
.
(Ⅰ)求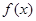 的单调区间;
的单调区间;
(Ⅱ)若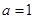 ,
,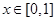 ,求函数
,求函数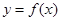 图象上任意一点处切线斜率
图象上任意一点处切线斜率 的取值范围.
的取值范围.
已知数列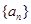 满足:
满足: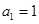 ,
,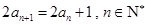 .数列
.数列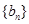 的前
的前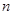 项和为
项和为 ,
,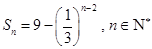 .
.
(Ⅰ)求数列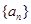 ,
,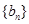 的通项公式;
的通项公式;
(Ⅱ)设 ,
,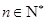 .求数列
.求数列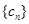 的前
的前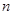 项和
项和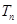 .
.
已知函数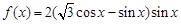 ,
,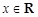 .
.
(Ⅰ)求函数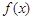 的最小正周期与单调增区间;
的最小正周期与单调增区间;
(Ⅱ)求函数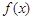 在
在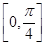 上的最大值与最小值.
上的最大值与最小值.
(本小题满分16分)已知数列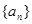 中,
中,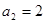 ,前
,前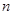 项和为
项和为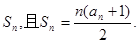
(Ⅰ)证明数列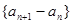 是等差数列,并求出数列
是等差数列,并求出数列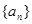 的通项公式;
的通项公式;
(Ⅱ)设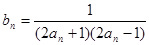 ,数列
,数列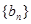 的前
的前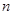 项和为
项和为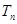 ,求使不等式
,求使不等式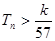 对一切
对一切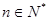 都成立的最大正整数
都成立的最大正整数 的值。
的值。