如图所示,水平面内有两根足够长的平行导轨L1、L2,其间距d=0.5m,左端接有容量C=2000μF的电容。质量m=20g的导体棒可在导轨上无摩擦滑动,导体棒和导轨的电阻不计。整个空间存在着垂直导轨所在平面的匀强磁场,磁感应强度B=2T。现用一沿导轨方向向右的恒力F1=0.44N作用于导体棒,使导体棒从静止开始运动,经t时间后到达B处,速度v=5m/s。此时,突然将拉力方向变为沿导轨向左,大小变为F2,又经2t时间后导体棒返回到初始位置A处,整个过程电容器未被击穿。求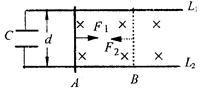
(1)导体棒运动到B处时,电容C上的电量;
(2)t的大小;
(3)F2的大小。
如图所示,摩托车运动员从高度h=5m的高台上水平飞出,跨越L=10m的壕沟。摩托车以初速度v0从坡底冲上高台的过程历时t=5s,发动机的功率恒为P=1.8kW。已知人和车的总质量为m=180kg(可视为质点),忽略一切阻力。取g=10m/s2。
(1)要使摩托车运动员从高台水平飞出刚好越过壕沟,求他离开高台时的速度大小。
(2)欲使摩托车运动员能够飞越壕沟,其初速度v0至少应为多大?
(3)为了保证摩托车运动员的安全,规定飞越壕沟后摩托车着地时的速度不得超过26m/s,那么,摩托车飞离高台时的最大速度vm应为多少?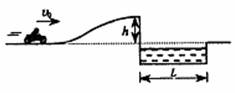
静止在水平地面上的木箱,质量m=50kg。若用F=400N的水平恒力推它,可以在5s内使它移动x=50m。
(1)求木箱与地面间的动摩擦因数 ;
;
(2)若用大小为400N、方向与水平方向夹角为37°(cos37°=0.8)斜向上的拉力拉木箱从静止开始运动,要使木箱能够到达50m远处,求木箱在拉力作用下移动的最小距离?(取g=10m/s2)
如图所示,ABC是光滑轨道,其中BC部分是半径为R的竖直放置的半圆.一质量为M的小木块放在轨道水平部分,木块被水平飞来的质量为m的子弹射中,并滞留在木块中.若被击中的木块沿轨道能滑到最高点C,已知木块对C点的压力大小为(M+m)g,求:子弹射入木块前瞬间速度的大小.
质量为1kg的物体在倾角30º为的光滑斜面(固定)顶端由静止释放,斜面高5m,求物体从斜面顶端滑到物体的动量变化底端过程中重力的冲量为多少?物体的动量变化为多少?
如图所示,质量为m的小物块在粗糙水平桌面上做直线运动,经距离l后以速度υ飞离桌面,最终落在水平地面上.已知l=1.4m,υ="3.0" m/s,m=0.10kg,物块与桌面间的动摩擦因数μ=0.25,桌面高h=0.45m,不计空气阻力,重力加速度g取10m/s2.求:
(1)小物块落地点距飞出点的水平距离s;
(2)小物块的初速度大小υ0.