直流电源的路端电压U="182" V。金属板AB、CD、EF、GH相互平行、彼此靠近。它们分别和变阻器上的触点a、b、c、d连接。变阻器上ab、bc、cd段电阻之比为1∶2∶3。孔O1正对B和E,孔O2正对D和G。边缘F、H正对。一个电子以初速度v0=4×106 m/s沿AB方向从A点进入电场,恰好穿过孔O1和O2后,从H点离开电场。金属板间的距离L1="2" cm,L2="4" cm,L3="6" cm。电子质量me=9.1×10-31 kg,电量q=1.6×10-19 C。正对两平行板间可视为匀强电场,(不计电子的重力)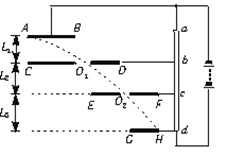
求:(1)各相对两板间的电场强度(小数点后保留2位)。
(2)电子离开H点时的动能。
(3)四块金属板的总长度(AB+CD+EF+GH)。
如图所示,匀强磁场竖直向上穿过水平放置的金属框架,框架宽为L,右端接有电阻为R,磁感应强度为B,一根质量为m、电阻不计的金属棒受到外力冲量后,以 的初速度沿框架向左运动,棒与框架的动摩擦因数为
的初速度沿框架向左运动,棒与框架的动摩擦因数为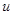 ,测得棒在整个运动过程中,通过任一截面的电量为q,求:(1)棒能运动的距离?(2)R上产生的热量?
,测得棒在整个运动过程中,通过任一截面的电量为q,求:(1)棒能运动的距离?(2)R上产生的热量?
由相同材料的木板搭成的轨道如图所示,其中木板AB、BC、CD、DE、EF┅长均为L=1.5m,木板OA和其它木板与水平地面的夹角都为β=370(sin370=0.6,con370=0.8),一个可看成质点的物体在木板OA上从图中的离地高度h=1.8m处由静止释放,物体与木板的动摩擦因数都为μ=0.2,在两木板交接处都用小曲面相连,使物体能顺利地经过它,既不损失动能,也不会脱离轨道。在以后的运动过程中,重力加速度取10m/s2,问: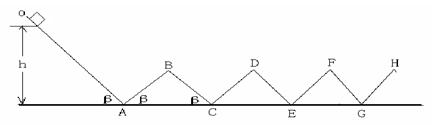
(1)物体能否静止在木板上?请说明理由。
(2)物体运动的总路程是多少?
(3)物体最终停在何处?并作出解释。
有一绝缘的、半径为R的光滑圆轨道固定在竖直平面内,在其圆心处固定一带正电的点电荷,现有一质量为m,带电量也为正电(其电量远小于圆心处的电荷,对圆心处电荷产生的电场影响很小,可忽略)的小球A,圆心处电荷对小球A的库仑力大小为F。开始小球A处在圆轨道内侧的最低处,如图所示。现给小球A一个足够大的水平初速度,小球A能在竖直圆轨道里做完整的圆周运动。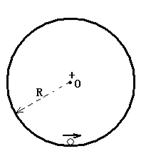
(1)小球A运动到何处时其速度最小?为什么?
(2)要使小球A在运动中始终不脱离圆轨道而做完整的圆周运动,小球A在圆轨道的最低处的初速度应满足什么条件?
有一个边长为L=1.6m的正方形桌子,桌面离地高度为h=1.25m。一个质量为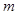 的小物块可从桌面正中心
的小物块可从桌面正中心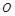 点以初速v0=3m/s沿着与OA成370的方向在桌面上运动直至落地。设动摩擦因数为μ="0.25" ,取g=10m/s2,求
点以初速v0=3m/s沿着与OA成370的方向在桌面上运动直至落地。设动摩擦因数为μ="0.25" ,取g=10m/s2,求
(1)物块离开桌面时速度是多少?
(2)物块落地的速度是多少?(可用根式表示)
(3)物块落地点到桌面中心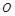 点的水平距离是多少?
点的水平距离是多少?
如图所示,楼梯口一倾斜的天花板与水平地面成θ=370,一装潢工人手持木杆绑着刷子粉刷天花板,工人所持木杆对刷子的作用力始终保持竖直向上,大小为F=10N,刷子的质量为m=0.5kg,刷子可视为质点,刷子与板间的动摩擦因数 =0.5,天花板长为L=4m,取g=10m/s2,试求:
=0.5,天花板长为L=4m,取g=10m/s2,试求: 
(1)刷子沿天花板向上的加速度。
(2)工人把刷子从天花板底端推到顶端所用的时间。