一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月产量如表（单位：辆）：
| |
轿车A |
轿车B |
轿车C |
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆。
（1）求z的值；
（2）用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率.
A、B两个试验方案在某科学试验中成功的概率相同，已知A、B两个方案至少一个方案试验成功的概率是0.36．
（1）求两个方案均获成功的概率；
（2）设试验成功的方案的个数为随机变量ξ，求ξ的分布列及数学期望．
在二项式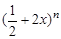
的展开式中，
（Ⅰ）若第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项；
（Ⅱ）若前三项的二项式系数和等于79，求展开式中系数最大的项．
已知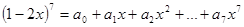
，求
（1）
的值。
（2）
的值。
（3）
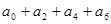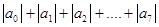的值。
已知函数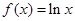
，
（1）求函数
的单调区间；
（2）当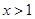
时，函数
恒成立，求实数
的取值范围；
（3）设正实数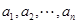
满足
．求证：
．
如图所示：已知过抛物线
的焦点F的直线
与抛物线相交于A，B两点。
（1）求证：以AF为直径的圆与x轴相切；
（2）设抛物线在A，B两点处的切线的交点为M，若点M的横坐标为2，求△ABM的外接圆方程；
（3）设过抛物线焦点F的直线与椭圆
的交点为C、D，是否存在直线使得
，若存在，求出直线的方程，若不存在，请说明理由。