为了实现“畅通市区”的目标,市地铁一号线准备动工,市政府现对地铁一号线第15标段工程进行招标,施工距离全长为300米.经招标协定,该工程由甲、乙两公司承建,甲、乙两公司施工方案及报价分别为:(1)甲公司施工单价y1(万元/米)与施工长度x(米)之间的函数关系为y1=27.8-0.09x,(2)乙公司施工单价y2(万元/米)与施工长度x(米)之间的函数关系为y2=15.8-0.05x.
(注:工程款=施工单价×施工长度)
(1)如果不考虑其他因素,单独由甲公司施工,那么完成此项工程需工程款多少万元?
(2)考虑到设备和技术等因素,甲公司必须邀请乙公司联合施工,共同完成该工程.因设备共享,两公司联合施工时市政府可节省工程款140万元(从工程款中扣除).
①如果设甲公司施工a米(0<a<300),那么乙公司施工______米,其施工单价y2=_______万元/米,试求市政府共支付工程款P(万元)与a(米)之间的函数关系式;
②如果市政府支付的工程款为2 900万元,那么应将多长的施工距离安排给乙公司施工?
如图1,AB是⊙O的直径,点C在⊙O上,且点C为弧BE的中点,连接AE并延长交BC延长线于点D.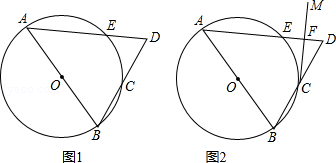
(1)判断△ABD的形状,并说明理由;
(2)过点C作CM⊥AD,垂足为点F,如图2.
①求证:CF是⊙O的切线;
②若⊙O的半径为3,DF=1,求sinB的值.
问题发现:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.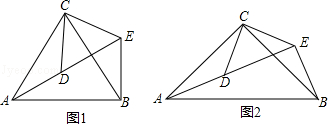
(1)求证:△ACD≌△BCE;
(2)求证:CD∥BE.
拓展探究:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,求∠AEB的度数.
假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:
| 单价/(元/千克) |
4 |
3 |
2 |
合计 |
| 小红购买的数量/千克 |
1 |
2 |
3 |
6 |
| 小慧购买的数量/千克 |
2 |
2 |
2 |
6 |
(1)小红和小慧购买西红柿数量的中位数是 ,众数是 ;
(2)从平均价格看,谁买的西红柿要便宜些.
小亮的说法
每次购买单价相同,购买总量也相同,平均价格应该也一样,都是(4+3+2)÷3=3(元/千克),所以两人购买的西红柿一样便宜.
小明的说法
购买的总量虽然相同,但小红花了16元,小慧花了18元,平均价格不一样,所以购买的西红柿便宜
思考小亮和小明的说法,你认为谁说得对?为什么?
(3)小明在直角坐标系中画出反比例函数的图象,图象经过点P(如图),点P的横、纵坐标分别为小红和小慧购买西红柿价格的平均数.
①求此反比例函数的关系式;
②判断点Q(2,5)是否在此函数图象上.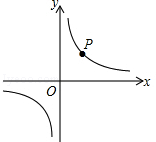
定义一种新运算“⊕”:a⊕b=a﹣2b,比如:2⊕(﹣3)=2﹣2×(﹣3)=2+6=8.
(1)求(﹣3)⊕2的值;
(2)若(x﹣3)⊕(x+1)=1,求x的值.
小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是
cm2.