2001年以来,我市药店积极实施药品降价,累计降价的总金额为269亿元. 五次药品降价的年份与相应降价金额如下表所示,表中缺失了2003年,2007年的相关数据. 已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额.
| 年份 |
2001 |
2003 |
2004 |
2005 |
2007 |
| 降价金额(亿元) |
54 |
|
35 |
40 |
|
在研究勾股定理时,同学们都见到过图1,∠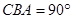 ,四边形
,四边形 、
、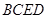 、
、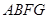 都是正方形.
都是正方形.
⑴连结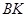 、
、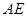 得到图2,则△
得到图2,则△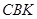 ≌△
≌△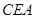 ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是
▲;过 作
作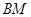 ⊥
⊥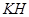 于
于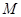 ,交
,交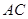 于
于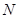 ,则
,则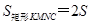 △
△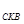 ;同理
;同理 △
△ ,得
,得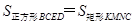 ,然后可证得勾股定理.
,然后可证得勾股定理.
⑵在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△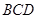 、△
、△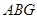 、△
、△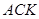 的面积关系是▲.
的面积关系是▲.
⑶为了研究问题的需要,将图1中的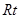 △
△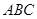 也进行“退化”为锐角△
也进行“退化”为锐角△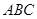 ,并擦去正方形
,并擦去正方形 得图4,由
得图4,由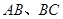 两边向三角形外作正△
两边向三角形外作正△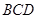 、正△
、正△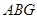 ,△
,△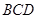 的外接圆与
的外接圆与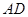 交于点
交于点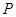 ,此时
,此时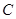 、
、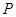 、
、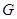 共线,从△
共线,从△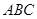 内一点到
内一点到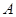 、
、 、
、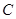 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点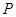 (已经被他人证明).设
(已经被他人证明).设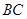 =3,
=3,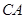 =4,
=4,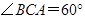 .求
.求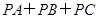 的值.
的值.
如图1,在平面上,给定了半径为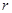 的⊙
的⊙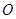 ,对于任意点
,对于任意点 ,在射线
,在射线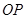 上取一点
上取一点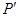 ,使得
,使得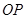 ·
· =
=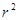 ,这种把点
,这种把点 变为点
变为点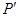 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点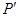 叫做互为反演点,⊙
叫做互为反演点,⊙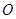 称为基圆.
称为基圆.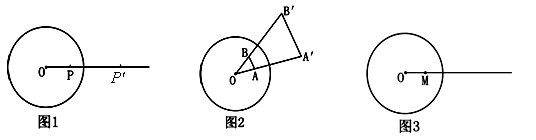
⑴如图2,⊙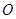 内有不同的两点
内有不同的两点 、
、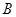 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是(▲)
一定相等的角是(▲)
A.∠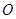 |
B.∠ |
C.∠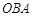 |
D.∠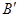 |
⑵如图3,⊙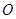 内有一点
内有一点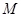 ,请用尺规作图画出点
,请用尺规作图画出点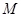 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).
⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆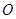 的半径为
的半径为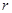 ,另一个半径为
,另一个半径为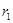 的⊙
的⊙ ,作射线
,作射线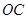 交⊙
交⊙ 于点
于点 、
、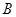 ,点
,点 、
、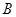 关于⊙
关于⊙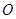 的反演点分别是
的反演点分别是 、
、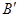 ,点
,点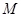 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙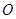 的反演点为
的反演点为 .求证:∠
.求证:∠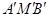 =90°.
=90°.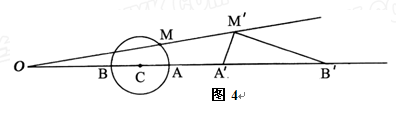
为了解某校九年级学生英语口语测试成绩情况,从中抽取部分学生的英语口语测试成绩统计如下图,现知道抽取的成绩中有12个满分(24分为满分).
⑴抽取了▲名学生的成绩;
⑵求所抽取的成绩的平均分;
⑶已知该校九年级共有650名学生,请估计该校九年级英语口语测试成绩在22分以上(不含22分)的人数. 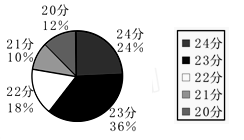
抛物线 与x轴交于
与x轴交于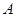 、
、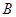 两点(点
两点(点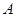 在点
在点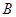 左边)与y轴交于点
左边)与y轴交于点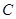 ,线段
,线段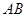 的中点为
的中点为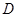 ,求
,求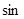 ∠
∠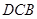 的值.
的值.
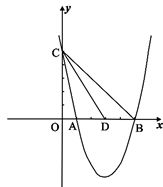 |
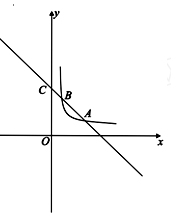
一次函数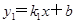 的图象与反比例函数
的图象与反比例函数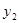 =
=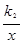 (
(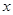 >0)的图象交于
>0)的图象交于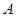 、
、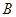 两点,与
两点,与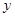 轴交于
轴交于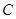 点,已知
点,已知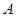 点坐标为(2,1),
点坐标为(2,1),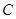 点坐标为(0,3). 求函数
点坐标为(0,3). 求函数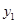 的表达式和
的表达式和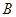 点的坐标
点的坐标