已知函数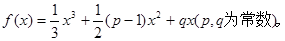
(1)若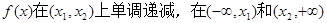 上单调递增,且
上单调递增,且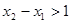 ,求证:
,求证: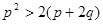
(2)若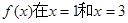 处取得极值,且在
处取得极值,且在 时,函数
时,函数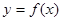 的图象在直线
的图象在直线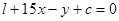 的下方,求c的取值范围.
的下方,求c的取值范围.
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业.分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(O<x<100).而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元.
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
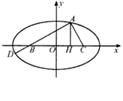
如图,直线l1与l2是同一平面内两条互相垂直的直线,交点是A,点B、D在直线l1上(B、D 位于点A右侧),且|AB|=4,|AD|=1,M是该平面上的一个动点,M在l1上的射影点是N,且|BN|=2|DM|.
(Ⅰ) 建立适当的坐标系,求动点M的轨迹C的方程.
(Ⅱ)过点D且不与l1、l2垂直的直线l交(Ⅰ)中的轨迹C于E、F两点;另外平面上的点G、H满足:① ②
②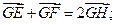 ③
③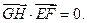 求点G的横坐标的取值范围.
求点G的横坐标的取值范围.
设 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线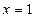 对称,证明
对称,证明 是周期函数.
是周期函数.
在直角坐标平面中, 的两个顶点分别
的两个顶点分别 的坐标为
的坐标为 ,
, ,平面内两点
,平面内两点 同时满足下列条件:
同时满足下列条件:
① ;②
;② ;③
;③ ∥
∥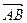
(1)求 的顶点
的顶点 的轨迹方程;
的轨迹方程;
(2)过点 的直线
的直线 与(1)中轨迹交于
与(1)中轨迹交于 两点,求
两点,求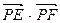 的取值范围
的取值范围
如图所示,B(– c,0),C(c,0),AH⊥BC,垂足为H,且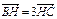 .
.
(1)若 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;
(2)D分有向线段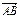 的比为
的比为 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤ ≤
≤ 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.