用反证法证明命题“三角形的内角至多有一个钝角”时,假设的内容应为( )
| A.假设至少有一个钝角 | B.假设至少有两个钝角 |
| C.假设没有一个钝角 | D.假设没有一个钝角或至少有两个钝角 |
下列各图是正方体或三棱锥, 、
、 、
、 、
、 分别是所在棱的中点,这四个点不共面的的图象共有
分别是所在棱的中点,这四个点不共面的的图象共有
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,已知棱长为a的正四面体ABCD中,E、F在BC上,G在AD上,E是BC的中点,CF= ,AG=
,AG= ,给出下列四个命题:①AC⊥BD,②FG=
,给出下列四个命题:①AC⊥BD,②FG=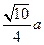 ,③侧面与底面所成二面角的余弦值为
,③侧面与底面所成二面角的余弦值为 ,④
,④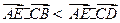 ,其中真命题的序号是()
,其中真命题的序号是()
| A.①②③ | B.①②④ | C.②③④ | D.①③④ |
在正三棱锥 中,
中, 、
、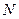 分别是棱
分别是棱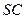 、
、 的中点,且
的中点,且 ,若侧棱
,若侧棱 ,则正三棱锥
,则正三棱锥 外接球的表面积是()
外接球的表面积是()
A.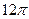 |
B. |
C.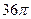 |
D. |
棱长为1的正方体ABCD-A1B1C1D1被以A为球心,AB为半径的球相截,则被截形体的表面积为()
A.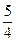 π π |
B. π π |
C.π | D. π π |
命题①空间直线a,b,c,若a∥b,b∥c则a∥c
②非零向量 ,若
,若 ∥
∥ ,
, ∥
∥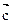 则
则 ∥
∥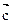
③平面α、β、γ若α⊥β,β⊥γ,则α∥γ
④空间直线a、b、c若有a⊥b,b⊥c,则a∥c
⑤直线a、b与平面β,若a⊥β,c⊥β,则a∥c
其中所有真命题的序号是()
| A.①②③ | B.①③⑤ | C.①②⑤ | D.②③⑤ |