设函数f(x)=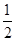 x2+2x+kln x,其中k≠0.
x2+2x+kln x,其中k≠0.
(1)当k>0时,判断f(x)在(0,+∞)上的单调性;
(2)讨论f(x)的极值点.
(本小题满分12分) 已知函数
(Ⅰ)将函数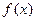 化简成
化简成 的形式,并指出
的形式,并指出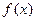 的最小正周期;
的最小正周期;
(Ⅱ)求函数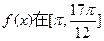 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知向量 与
与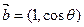 互相垂直,其中
互相垂直,其中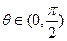 .
.
(1)求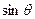 和
和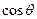 的值;
的值;
(2)若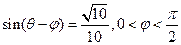 ,求
,求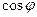 的值.
的值.
(本小题 满分13分)
满分13分)
已知函数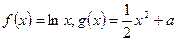 (
(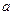 为常数),直线l与函数
为常数),直线l与函数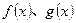 的图象都相切,且l与函数
的图象都相切,且l与函数 的图象的切点的横坐标为l.
的图象的切点的横坐标为l.
(Ⅰ)求直线l的方程及a的值;
(Ⅱ)当k>0时,试讨论方程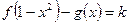 的解的个数.
的解的个数.
(本小题满分13分)
某地建一座桥,两端的桥墩已建好,这两墩相距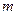 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为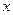 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为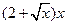 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为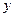 万元。
万元。
(Ⅰ)试写出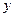 关于
关于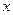 的函数关系式;
的函数关系式;
(Ⅱ)当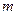 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使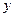 最小?
最小?
已知集合A= ,B=
,B=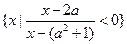 .
.
⑴当a=2时,求A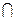 B;⑵求使B
B;⑵求使B A的实数a的取值范围.
A的实数a的取值范围.