在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
八年级数学课上,曹老师出示了如下框中的题目.(本题8分)
小聪与同桌小明讨论后,进行了如下解答:
(1)特殊情况·探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE_______DB(填“>”,“<”或“=” ).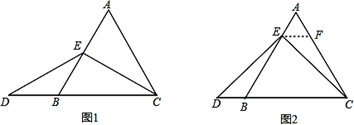
(2)特例启发·解答题目
解:题目中, AE与DB的大小关系是:AE_____DB(填“>”,“<”或“=” ).
理由如下:如图2,过点E作EF∥BC,交AC于点F,
(请你完成以下解答过程)
(3)拓展结论·设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.
若△ABC的边长为2,AE=4,求CD的长(请你直接写出结果).
(本题6分)如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将一块三角板中含45°角的顶点放在A上,从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.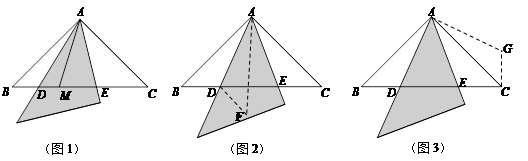
(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2.同组的小颖和小亮随后想出了两种不同的方法进行解决;小颖的想法:将△ABD沿AD所在的直线对折得到△ADF(如图2);小亮的想法:将△ABD绕点A顺时针旋转90°得到△ACG(如图3).请你选择其中的一种方法证明小敏的发现的是正确的.
(本题8分)(1)如图(1),已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(尺规作图,不写作法,保留作图痕迹,写出结论);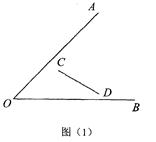
(2)如图(2),以数轴的单位长线段为边作两个正方形,以数轴的原点为圆心,矩形对角线为半径画弧,交数轴负半轴于点A,则在数轴上A表示的数是,请仿照以上方法画出在数轴上表示的数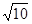 的点B.
的点B.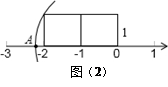
(3)如图,Rt△ABC中,∠C=90°,AC=4,BC=3,以△ABC的一边为边画等腰三角形,使它的第三个顶点在△ABC的其它边上.请在图①、图②、图③中分别画出一个符合条件的等腰三角形,且三个图形中的等腰三角形各不相同,并在图下方的横线上写明所画等腰三角形的腰和腰长(不要求尺规作图).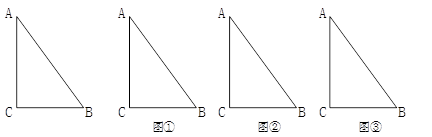
图①图②图③
(本题4分)如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,求∠ABC的度数.
已知:如图,O为数轴的原点,A,B分别为数轴上的两点,A点对应的数为-30,B点对应的数为100.
(1)A、B间的距离是;
(2)若点C也是数轴上的点,C到B的距离是C到原点O的距离的3倍,求C对应的数;
(3)若当电子P从B点出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4个单位长度/秒的速度向左运动,设两只电子蚂蚁在数轴上的D点相遇,那么D点对应的数是多少?
(4)若电子蚂蚁P从B点出发,以8个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从A点出,以4个单位长度/秒向右运动.设数轴上的点N到原点O的距离等于P点到O的距离的一半,有两个结论①ON+AQ的值不变;②ON-AQ的值不变.请判断那个结论正确,并求出结论的值.