今年我市水果大丰收,A、B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基础运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件。
(1)设从A基础运往甲 销售点水果x件,总运费为w元,请用含x的代数式表示w,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费。
如图,已知 是 的直径,点 是圆上异于 、 的一点,连结 并延长至点 ,使 ,连结 交 于点 ,连结 .
(1)求证: 是等腰三角形;
(2)连结 并延长,与以 为切点的切线交于点 ,若 , ,求 的长.

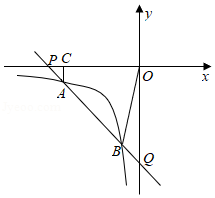
如图,一次函数 的图象与反比例函数 的图象相交于点 , 两点,过点 作 于点 .
(1)求一次函数和反比例函数的表达式;
(2)求四边形 的面积.
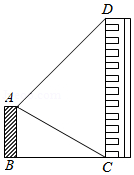
如图, 和 两幢楼地面距离 为 米,楼 高30米,从楼 的顶部点 测得楼 的顶部点 的仰角为 .
(1)求 的大小;
(2)求楼 的高度(结果保留根号).
在疫情期间,为落实“停课不停学”,某校对本校学生某一学科在家学习情况进行抽样调查,了解到学生的学习方式有:电视直播、任课教师在线辅导、教育机构远程教学、自主学习.参与调查的学生只能选择一种学习方式,将调查结果绘制成不完整的扇形统计图和条形统计图.根据如图所示的统计图,解答下列问题.
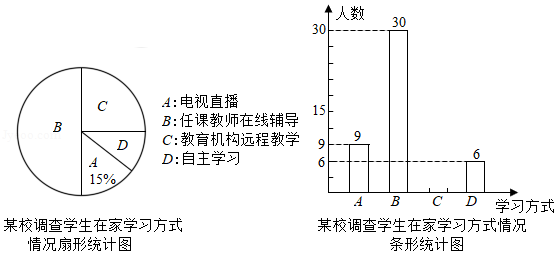
(1)本次接受调查的学生有 名;
(2)补全条形统计图;
(3)根据调查结果,若本校有1800名学生,估计有多少名学生参与任课教师在线辅导?
如图,在 中,点 是边 的中点,连结 并延长到点 ,使 ,连结 .
(1)求证: ;
(2)若 的面积为5,求 的面积.
