类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.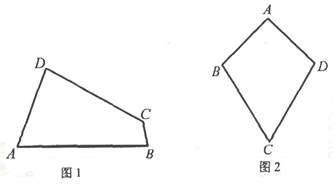
为了解全市居民用户用电情况,某部门从居民用户中随机抽取100户进行月用电量(单位: 调查,按月用电量 , , , , , 进行分组,绘制频数分布直方图如图.

(1)求频数分布直方图中 的值;
(2)判断这100户居民用户月用电量数据的中位数在哪一组(直接写出结果);
(3)设各组居民用户月平均用电量如表:
|
组别 |
|
|
|
|
|
|
|
月平均用电量(单位: |
75 |
125 |
175 |
225 |
275 |
325 |
根据上述信息,估计该市居民用户月用电量的平均数.
如图,圆 中两条互相垂直的弦 , 交于点 .
(1) 是 的中点, , ,求圆 的半径长;
(2)点 在 上,且 ,求证: .

)已知正比例函数 与反比例函数 的图象都经过点 .
(1)求 , 的值;
(2)在图中画出正比例函数 的图象,并根据图象,写出正比例函数值大于反比例函数值时 的取值范围.

某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
观察思考
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图 ;当正方形地砖有2块时,等腰直角三角形地砖有8块(如图 ;以此类推.

规律总结
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加 块;
(2)若一条这样的人行道一共有 为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 (用含 的代数式表示).
问题解决
(3)现有2021块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?
学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形 为矩形,点 、 分别在 、 上, , , , .求零件的截面面积.参考数据: , .
