如图，在平面直角坐标系中，A是抛物线
上的一个动点，且点A在第一象限内．AE⊥y轴于点E，点B坐标为(O，2)，直线AB交
轴于点C，点D与点C关于y轴对称，直线DE与AB相交于点F，连结BD．设线段AE的长为m，△BED的面积为S．
（1）当
时，求S的值．
（2）求S关于
的函数解析式．
（3）①若S＝
时，求
的值；
②当m＞2时，设
，猜想k与m的数量关系并证明．
如图，直线DE交△ABC的边AB、AC于D、E，交BC延长线于F，若∠B＝67°，∠ACB＝74°，∠AED＝48°，求∠BDF的度数．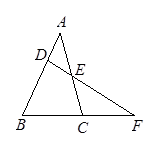
解下列方程组：
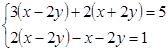⑴、
⑵、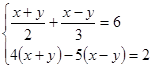
( 7分)如图，AB∥CD，分别写出下面四个图形中∠A与∠P、∠C的关系，请你从所得到的关系中任选一图的结论说明理由。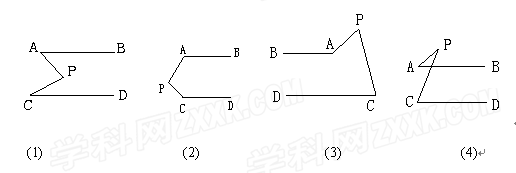
⑴⑵
⑶⑷
( 4分)如图，EF//AD，
＝
.说明：∠DGA+∠BAC=180°.请将说明过程填写完成.
解：∵EF//AD，（已知）
∴＝_____.(_____________________________)
.
又∵＝，（______）
∴＝
，（________________________）.
∴AB//______，(____________________________)
∴∠DGA+∠BAC=180°.(_____________________________)
按要求画图：将下图中的阴影部分向右平移6个单位，再向下平移4个单位。