( 4分)如图，EF//AD，
＝
.说明：∠DGA+∠BAC=180°.请将说明过程填写完成.
解：∵EF//AD，（已知）
∴＝_____.(_____________________________)
.
又∵＝，（______）
∴＝
，（________________________）.
∴AB//______，(____________________________)
∴∠DGA+∠BAC=180°.(_____________________________)
如图，经过原点的抛物线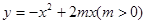
与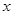
轴的另一个交点为A.过点P(1,
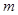)作直线PM⊥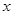轴于点M，交抛物线于点B．记点B关于抛物线对称轴的对称点为C(B、C不重合)．连结CB，CP．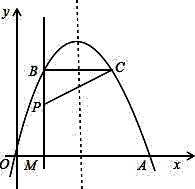
（1）当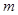＝3时，求点A的坐标和BC的长；
（2）当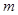>1时，连结CA，当CA⊥CP时，求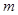的值．
（3）过点P作PE⊥PC且PE =PC，问是否存在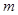，使得点E落x轴在上？若存在，求出所有满足要求的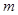的值，并写出相对应的点E坐标；若不存在，请说明理由．
如图，△ABC中，E是AC上一点，且AE =AB，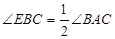
,以AB为直径的⊙
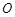交AC于点D，交EB于点F．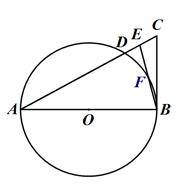
(1)求证：BC与⊙O相切；
(2)若AB=8，sin∠EBC=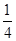
,求AC的长．
某私营服装厂根据2014年市场分析，决定2015年调整服装制作方案，准备每周（按120工时计算）制作西服、休闲服、衬衣共360件，且衬衣至少60件。已知每件服装的收入和所需工时如下表：
| 服装名称 |
西服 |
休闲服 |
衬衣 |
| 工时/件 |
 |
 |
 |
| 收入（百元）/件 |
3 |
2 |
1 |
设每周制作西服x件，休闲服y件，衬衣z件。
(1)请你分别从件数和工时数两个方面用含有x、y 的代数式表示衬衣的件数z。
(2)求y与x之间的函数关系式。
(3)问每周制作西服、休闲服、衬衣各多少件时，才能使总收入最高？最高总收入是多少？
如图，将矩形ABCD沿直线EF折叠，使点C与点A重合，折痕交AD于点E、交BC于点F，连接AF、CE．
(1)求证：四边形AFCE为菱形；
(2)设AE=a，ED=b，DC=c.请写出一个a、b、c三者之间的数量关系式，并说明理由。
如图，在由边长为1的小正方形组成的网格中，三角形ABC的顶点均落在格点上．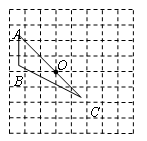
（1）将△ABC绕点O顺时针旋转90°后，得到△A1B1C1．在网格中画出△A1B1C1；
（2）求线段OA在旋转过程中扫过的图形面积；（结果保留
）
（3）求∠BCC1的正切值．