如图,△ABC中,E是AC上一点,且AE =AB,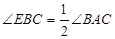 ,以AB为直径的⊙
,以AB为直径的⊙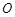 交AC于点D,交EB于点F.
交AC于点D,交EB于点F.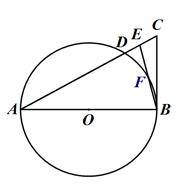
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC=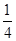 ,求AC的长.
,求AC的长.
如图,河流两岸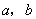 互相平行,C,D是河岸
互相平行,C,D是河岸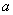 上间隔50m的两个电线杆,某人在河岸
上间隔50m的两个电线杆,某人在河岸 上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值(结果精确到个位).
上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值(结果精确到个位).
已知二次函数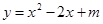 的图象C1与x轴有且只有一个公共点,求C1的顶点坐标,并在图中画出C1的图象.
的图象C1与x轴有且只有一个公共点,求C1的顶点坐标,并在图中画出C1的图象.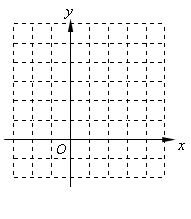
如图,A、B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率.
计算:  .
.
已知线段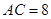 ,
, .
.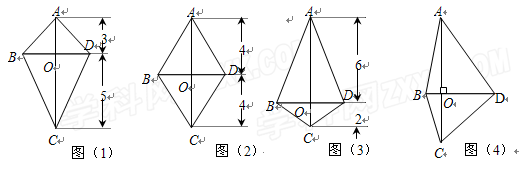
(1)已知线段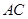 垂直于线段
垂直于线段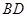 .设图(1)、图(2)和图(3)中的四边形
.设图(1)、图(2)和图(3)中的四边形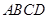 的
的
面积分别为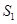 ,
,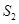 和
和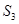 ,则
,则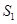 = ,
= ,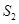 = ,
= ,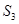 = ;
= ;
(2)如图(4),对于线段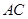 与线段
与线段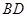 垂直相交(垂足
垂直相交(垂足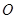 不与点
不与点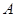 ,
,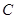 ,
,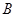 ,
,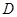 重合)的任意情形,请你就四边形
重合)的任意情形,请你就四边形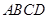 面积的大小提出猜想,并证明你的猜想.
面积的大小提出猜想,并证明你的猜想.