已知线段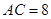 ,
, .
.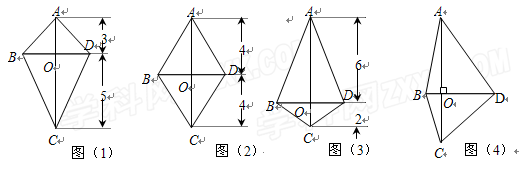
(1)已知线段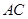 垂直于线段
垂直于线段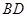 .设图(1)、图(2)和图(3)中的四边形
.设图(1)、图(2)和图(3)中的四边形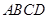 的
的
面积分别为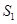 ,
,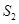 和
和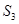 ,则
,则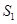 = ,
= ,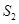 = ,
= ,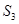 = ;
= ;
(2)如图(4),对于线段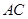 与线段
与线段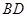 垂直相交(垂足
垂直相交(垂足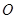 不与点
不与点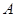 ,
,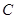 ,
,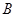 ,
,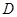 重合)的任意情形,请你就四边形
重合)的任意情形,请你就四边形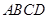 面积的大小提出猜想,并证明你的猜想.
面积的大小提出猜想,并证明你的猜想.
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高 米,且AC=
米,且AC= 米,设太阳光线与水平地面的夹角为
米,设太阳光线与水平地面的夹角为 .当
.当 时,测得楼房在地面上的影长AE=
时,测得楼房在地面上的影长AE= 米,现有一只小猫睡在台阶的MN这层上晒太阳.(
米,现有一只小猫睡在台阶的MN这层上晒太阳.( 取
取 )
)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当 时,问小猫能否还晒到太阳?请说明理由.
时,问小猫能否还晒到太阳?请说明理由.
如图,在平面直角坐标系xOy中,已知正比例函数 与一次函数
与一次函数 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设 轴上一点P(
轴上一点P( ,0),过点P作
,0),过点P作 轴的垂线(垂线位于点A的右侧),分别交
轴的垂线(垂线位于点A的右侧),分别交 和
和 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC= OA,求△OBC的面积.
OA,求△OBC的面积.
如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:直线ED与⊙O相切.
有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字 和
和 ;乙袋中有三个完全相同的小球,分别标有数字
;乙袋中有三个完全相同的小球,分别标有数字 、
、 和
和 .小丽先从甲袋中随机取出一个小球,记下小球上的数字为
.小丽先从甲袋中随机取出一个小球,记下小球上的数字为 ;再从乙袋中随机取出一个小球,记录下小球上的数字为
;再从乙袋中随机取出一个小球,记录下小球上的数字为 ,设点P的坐标为(
,设点P的坐标为( ,
, ).
).
(1)请用表格或树状图列出点P所有可能的坐标;
(2)求点P在一次函数 图像上的概率.
图像上的概率.
先化简,再求值: ,其中
,其中 .
.